Giải bài 45 trang 23 sách bài tập toán 11 - Cánh diều
Từ đồ thị hàm số \(y = \cos x\), cho biết:
Đề bài
Từ đồ thị hàm số \(y = \cos x\), cho biết:
a) Có bao nhiêu giá trị của \(x\) trên đoạn \(\left[ { - 5\pi ;0} \right]\) để \(\cos x = 1\)?
b) Có bao nhiêu giá trị của \(x\) trên khoảng \(\left( { - \frac{{9\pi }}{2}; - \frac{{3\pi }}{2}} \right)\) để \(\cos x = 0\)?
Phương pháp giải - Xem chi tiết
Vẽ đồ thị hàm số \(y = \cos x\)
a) Vẽ đường thẳng \(y = 1\) và đếm số giao điểm của đường thẳng này với đồ thị hàm số \(y = \cos x\).
b) Vẽ đường thẳng \(y = 0\) và đếm số giao điểm của đường thẳng này với đồ thị hàm số \(y = \cos x\).
Lời giải chi tiết
a) Ta có hình vẽ sau:
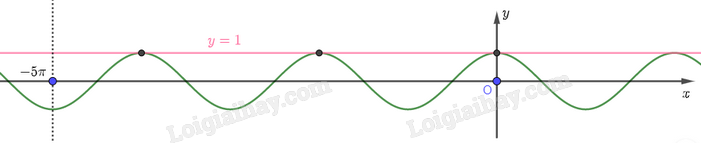
Dựa vào hình vẽ, ta thấy đường thẳng \(y = 1\) cắt đồ thị hàm số \(y = \cos x\) tại 3 điểm có hoành độ nằm trên đoạn \(\left[ { - 5\pi ;0} \right]\), nghĩa là có 3 giá trị của \(x\) trên đoạn \(\left[ { - 5\pi ;0} \right]\) để \(\cos x = 1\).
b) Ta có hình vẽ sau:
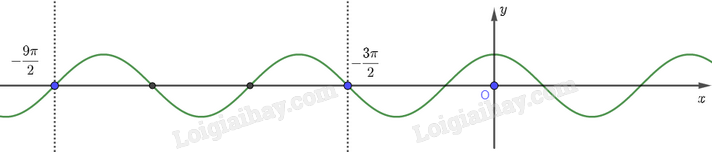
Từ hình vẽ trên, ta thấy đường thẳng \(y = 0\) (trục \(Ox\)) cắt đồ thị hàm số \(y = \cos x\) tại 3 điểm có hoành độ nằm trên khoảng \(\left( { - \frac{{9\pi }}{2}; - \frac{{3\pi }}{2}} \right)\), nghĩa là có 2 giá trị của \(x\) trên khoảng \(\left( { - \frac{{9\pi }}{2}; - \frac{{3\pi }}{2}} \right)\) để \(\cos x = 0\). (Lưu ý rằng chúng ta không lấy những giá trị \(x = - \frac{{9\pi }}{2}\) và \(x = - \frac{{3\pi }}{2}\))
Search google: "từ khóa + timdapan.com" Ví dụ: "Giải bài 45 trang 23 sách bài tập toán 11 - Cánh diều timdapan.com"







