Bài 44 trang 90 Vở bài tập toán 7 tập 2
Giải bài 44 trang 90 VBT toán 7 tập 2. Cho hai điểm M, N nằm trên đường trung trực của đoạn thẳng AB. Chứng minh tam giác AMN bằng tam giác BMN...
Đề bài
Cho hai điểm \(M, N\) nằm trên đường trung trực của đoạn thẳng \(AB\). Chứng minh \(∆AMN = ∆BMN.\)
Phương pháp giải - Xem chi tiết
Áp dụng định lí 1: Điểm nằm trên đường trung trực của một đoạn thẳng thì cách đều hai mút của đoạn thẳng đó.
Lời giải chi tiết
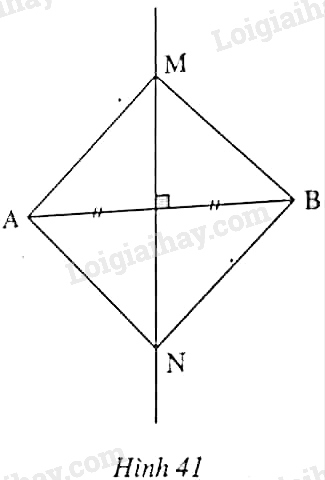
Theo giả thiết, điểm \(M\) nằm trên đường trung trực của \(AB\) nên điểm \(M\) cách đều hai điểm \(A;B\) (theo tính chất đường trung trực), hay \(MA = MB\).
Tương tự điểm \(N\) cách đều hai điểm \(A;B\) nên \(NA = NB\).
Hai tam giác \(AMN\) và \(BMN\) có \(MA = MB\); \(NA = NB\); \(MN\) chung nên \(∆AMN = ∆BMN\) (c.c.c).
Mẹo Tìm đáp án nhanh nhất
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 44 trang 90 Vở bài tập toán 7 tập 2 timdapan.com"
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 44 trang 90 Vở bài tập toán 7 tập 2 timdapan.com"







