Bài 41 trang 143 Vở bài tập toán 8 tập 2
Giải bài 41 trang 143 VBT toán 8 tập 2. A, B, C, D là các đỉnh của một hình hộp chữ nhật...
Đề bài
\(A, B, C, D\) là các đỉnh của một hình hộp chữ nhật. Hãy quan sát hình 145 rồi điền số thích hợp vào các ô trống ở bảng sau:
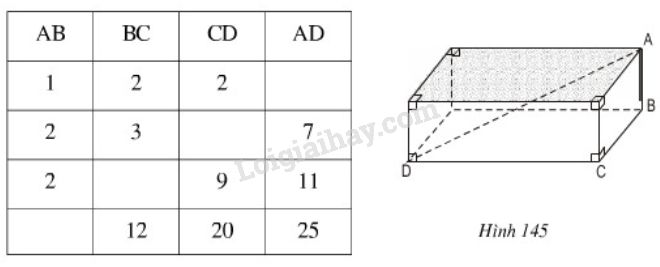
Phương pháp giải - Xem chi tiết
Áp dụng định lí Pi-ta-go.
Lời giải chi tiết
Ở ô (I):\(AD = \sqrt {A{B^2} + B{C^2} + C{D^2}}\)
\( = \sqrt {{1^2} + {2^2} + {2^2}} = \sqrt 9 = 3\)
Ở ô (II):\(BD = \sqrt {A{D^2} - A{B^2}} = \sqrt {{7^2} - {2^2}} \) \(= \sqrt {45} \)
\(CD = \sqrt {B{D^2} - B{C^2}} = \sqrt {45 - {3^2}}\) \( = \sqrt {36} = 6\)
Ở ô (III):\(BD = \sqrt {A{D^2} - A{B^2}} = \sqrt {{{11}^2} - {2^2}} \) \(= \sqrt {117} \)
\(BC = \sqrt {B{D^2} - D{C^2}}\)
\( = \sqrt {117 - {9^2}} = \sqrt {117 - 81} \)\(\,= \sqrt {36} = 6\)
Ở ô (IV):\(BD = \sqrt {D{C^2} + B{C^2}}\)
\( = \sqrt {{{20}^2} + {{12}^2}} = \sqrt {400 + 144} = \sqrt {544} \)
\(AB = \sqrt {A{D^2} - B{D^2}} = \sqrt {{{25}^2} - 544}\) \( = \sqrt {81} = 9\)
Vậy ta được kết quả ở bảng sau:
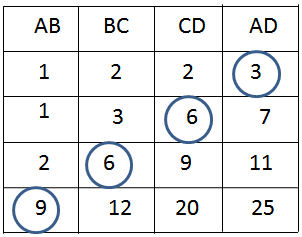
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 41 trang 143 Vở bài tập toán 8 tập 2 timdapan.com"







