Bài 38 trang 140 Vở bài tập toán 8 tập 2

Tính diện tích xung quanh, diện tích toàn phần và thể tích của lăng trụ đứng có chiều cao \(h\) và đáy lần lượt là:

LG a

Hình vuông cạnh \(a\);

Phương pháp giải:

Áp dụng công thức tính diện tích xung quanh, diện tích toàn phần và thể tích của lăng trụ đứng.

Giải chi tiết:

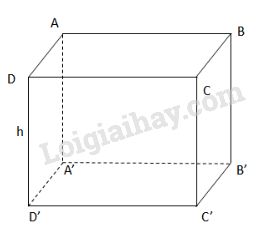
Kí hiệu lăng trụ đứng đã cho như hình bên. 

Diện tích xung quanh là:

\({S_{xq}} = 2p.h = 4.a.{\text{ }}h\)

Diện tích một đáy là :

\({S_đ} = {a^2}\)

Diện tích toàn phần của lăng trụ đứng là :

\({S_{tp}} = {S_{xq}} + 2{S_đ} = 4ah + 2{a^2}\)

Thể tích lăng trụ :

\(V = {S_đ}h = {a^2}.h\)

LG b

 Tam giác đều cạnh \(a\);

Phương pháp giải:

Áp dụng công thức tính diện tích xung quanh, diện tích toàn phần và thể tích của lăng trụ đứng.

Giải chi tiết:

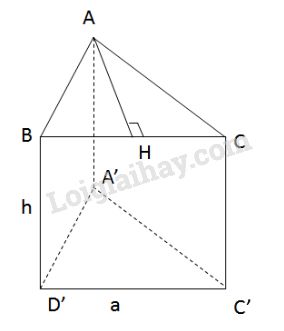
Chiều cao của tam giác đều là:

 \(AH = \sqrt {A{B^2} - B{H^2}}  = \sqrt {{a^2} - {{\left( {\dfrac{a }{ 2}} \right)}^2}} \) \(  = \sqrt {\dfrac{{3{a^2}}}{4}}  = \dfrac{{a\sqrt 3 }}{2}\)

Diện tích xung quanh là:

\({S_{xq}} = 2p.h = 3a.h\) 

Diện tích một đáy là:

\({S_đ} = \dfrac{1}{2}a.\dfrac{{a\sqrt 3 }}{2} = \dfrac{{{a^2}\sqrt 3 }}{4}\)

Diện tích toàn phần là:

\({S_{tp}} = {S_{xq}} + 2{S_đ}=3ah +2.\dfrac{{{a^2}\sqrt 3 }}{4}\)\(\, = 3ah + \dfrac{{{a^2}\sqrt 3 }}{2}\)

Thể tích: \(V = {S_đ}.h = \dfrac{{{a^2}\sqrt 3 }}{4}.h = \dfrac{{{a^2}h\sqrt 3 }}{4}\)

LG c

Lục giác đều cạnh \(a\); 

Phương pháp giải:

Áp dụng công thức tính diện tích xung quanh, diện tích toàn phần và thể tích của lăng trụ đứng.

Giải chi tiết:

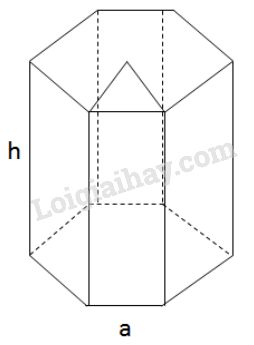
Diện tích xung quanh là:

\({S_{xq}}= 2p. h = 6a.h\)

Diện tích tam giác đều cạnh a (theo câu b) là \(\dfrac{{{a^2}\sqrt 3 }}{4}\).

Do đó diện tích một đáy của lăng trụ là :

 \({S_đ} = 6.\dfrac{{{a^2}\sqrt 3 }}{4} = \dfrac{{3{a^2}\sqrt 3 }}{2}\)

Diện tích toàn phần là: \({S_{tp}} = {S_{xq}} + 2{S_đ}\) 

 \({S_{tp}} = 6ah + 2.\dfrac{{3{a^2}\sqrt 3 }}{2} = 6ah + 3{a^2}\sqrt 3 \)\(\, = 3a\left( {2h + a\sqrt 3 } \right)\)

Thể tích tích lăng trụ :

 \(V = {S_đ}.h = \dfrac{{3{a^2}\sqrt 3 }}{2}.h = \dfrac{{3{a^2}h\sqrt 3 }}{2}\)

LG d

 Hình thang cân, đáy lớn là \(2a\), các cạnh còn lại bằng \(a\); 

Phương pháp giải:

Áp dụng công thức tính diện tích xung quanh, diện tích toàn phần và thể tích của lăng trụ đứng.

Giải chi tiết:

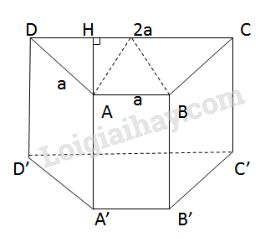
Diện tích xung quanh : 

\({S_{xq}}= 2ph = (2a + a +a +a). h \)\(\,= 5ah\).

Chiều cao hình thang cũng chính là chiều cao tam giác đều cạnh \(a\).

 \(AH = \dfrac{{a\sqrt 3 }}{2}\) (theo câu b)

Diện tích một đáy hình lăng trụ là:

 \({S_đ} = \dfrac{{\left( {2a + a} \right).AH}}{2} \)\(\,= \dfrac{{3a}}{2}.\dfrac{{a\sqrt 3 }}{2} = \dfrac{{3{a^2}\sqrt 3 }}{4}\)

Diện tích toàn phần là:

 \({S_{tp}} = {S_{xq}} + 2{S_đ} = 5ah + 2.\dfrac{{3{a^2}\sqrt 3 }}{4} \)\(\,= 5ah + \dfrac{{3{a^2}\sqrt 3 }}{2}\)

Thể tích hình lăng trụ:

 \(V = S.h = \dfrac{{3{a^2}\sqrt 3 }}{4}.h = \dfrac{{3{a^2}h\sqrt 3 }}{4}\)

LG e

Hình thoi có hai đường chéo là \(6a\) và \(8a\). 

Phương pháp giải:

Áp dụng công thức tính diện tích xung quanh, diện tích toàn phần và thể tích của lăng trụ đứng.

Giải chi tiết:

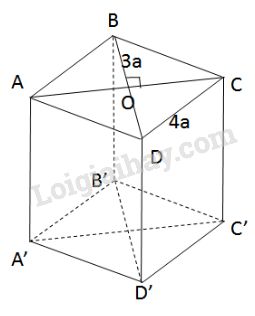
Cạnh của hình thoi: 

 \(BC = \sqrt {O{B^2} + O{C^2}}  \) \(= \sqrt {{{\left( {3a} \right)}^2} + {{\left( {4a} \right)}^2}}  \) \(= \sqrt {25{a^2}}  = 5a\)

Diện tích xung quanh lăng trụ:

\(S_{xq}= 2ph = 4.5a.h = 20ah\)

Diện tích một đáy của lăng trụ:

\({S_đ} = \dfrac{1}{2}.6a.8a = 24{a^2}\)

Diện tích toàn phần:

\({S_{tp}} = {S_{xq}} + 2{S_đ} \)\(\,= 20ah + 2.24a = 20ah + 48{a^2}\)

Thể tích lăng trụ:

\(V = Sh =24{a^2}.h\)