Bài 41 trang 59 Vở bài tập toán 7 tập 2
Giải bài 41 trang 59 VBT toán 7 tập 2.Trong các số cho bên phải mỗi đa thức, số nào là nghiệm của đa thức đó ? ...
Đề bài
Trong các số cho bên phải mỗi đa thức, số nào là nghiệm của đa thức đó?
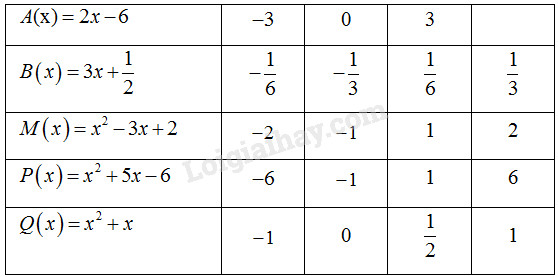
Phương pháp giải - Xem chi tiết
Muốn kiểm tra một số \(a\) có phải là nghiệm của đa thức \(f(x)\) không ta làm như sau:
• Tính \(f(a)=?\) (giá trị của \(f(x)\) tại \(x = a\))
• Nếu \(f(a)= 0\) \( \Rightarrow a\) là nghiệm của \(f(x)\)
• Nếu \(f(a)≠0 \Rightarrow a\) không phải là nghiệm của \(f(x)\).
Lời giải chi tiết
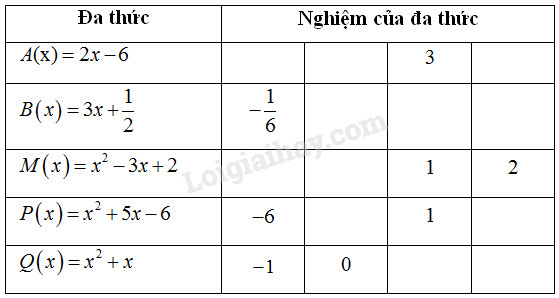
Giải thích:
a) Ta có:
\(\eqalign{
& A\left( { - 3} \right) = 2.\left( { - 3} \right) - 6 = - 6 - 6 \cr&\;\;\;\;\;\;\;\;\;\;\;\;= - 12 \cr
& A\left( 0 \right) = 2.0 - 6 = 0 - 6 = - 6 \cr
& A\left( 3 \right) = 2.3 - 6 = 6 - 6 = 0 \cr} \)
Vậy \(A(x) = 2x - 6\) có nghiệm là \(3\)
b) Ta có:
\(\eqalign{
& B\left( {{{ - 1} \over 6}} \right) = 3.\left( {{{ - 1} \over 6}} \right) + {1 \over 2} \cr& \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \;\;\;\;\;= {{ - 3} \over 6} + {1 \over 2} \cr
& \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \;\;\;\;\;= {{ - 1} \over 2} + {1 \over 2} = 0 \cr
& B\left( {{{ - 1} \over 3}} \right) = 3.\left( {{{ - 1} \over 3}} \right) + {1 \over 2}\cr&\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \;\;\;\;\; = {{ - 3} \over 3} + {1 \over 2} \cr
& \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \;\;\;\;\;= - 1 + {1 \over 2} \cr&\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \;\;\;\;\;= {{ - 2} \over 2} + {1 \over 2} = {{ - 1} \over 2} \cr
& B\left( {{1 \over 6}} \right) = 3.{1 \over 6} + {1 \over 2} = {3 \over 6} + {1 \over 2} \cr
& \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\;\;\; = {1 \over 2} + {1 \over 2} = 1 \cr
& B\left( {{1 \over 3}} \right) = 3.{1 \over 3} + {1 \over 2} = {3 \over 3} + {1 \over 2} \cr
& \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\;\;\;\; = 1 + {1 \over 2} = {2 \over 2} + {1 \over 2} = {3 \over 2} \cr} \)
\(B(x) = 3x + \dfrac{1}{2}\) có nghiệm là \( - \dfrac{1}{6}\)
c) Ta có:
\(M\left( { - 2} \right) = {\left( { - 2} \right)^2} - 3.\left( { - 2} \right) + 2\)\(\, = 4 + 6 + 2 = 12 \)
\(M\left( { - 1} \right) = {\left( { - 1} \right)^2} - 3.\left( { - 1} \right) + 2 \)\(\,= 1 + 3 + 2 = 6 \)
\(M\left( 1 \right) = {1^2} - 3.1 + 2 = 1 - 3 + 2 = 0 \)
\(M\left( 2 \right) = {2^2} - 3.2 + 2 = 4 - 6 + 2 = 0 \)
\(M\left( x \right) = {x^2}-3x + 2\) có nghiệm là \(1\) và \(2\).
d) Ta có:
\( P\left( { - 6} \right) = {\left( { - 6} \right)^2} + 5.\left( { - 6} \right) - 6 \)\(\,= 36 - 30 - 6 = 0 \)
\(P\left( { - 1} \right) = {\left( { - 1} \right)^2} + 5.\left( { - 1} \right) - 6 \)\(\,= 1 - 5 - 6 = - 10 \)
\(P\left( 1 \right) = {1^2} + 5.1 - 6 \)\(\,= 1 + 5 - 6 = 0 \)
\( P\left( 6 \right) = {6^2} + 5.6 - 6 \)\(\,= 36 + 30 - 6 = 60\)
\(P\left( x \right) = {x^2} + 5x - 6\) có nghiệm là \(1\) và \(-6\).
e) Ta có:
\( Q\left( { - 1} \right) = {\left( { - 1} \right)^2} + \left( { - 1} \right)\)\(\, = 1 + \left( { - 1} \right) = 0 \)
\(Q\left( 0 \right) = {0^2} + 0 = 0 \)
\(\displaystyle Q\left( {{1 \over 2}} \right) = {\left( {{1 \over 2}} \right)^2} + {1 \over 2}\)\(\,\displaystyle= {1 \over 4} + {1 \over 2} = {3 \over 4} \)
\(Q\left( 1 \right) = {1^2} + 1 = 1 + 1 = 2\)
\(Q\left( x \right) = {x^2} + x\) có nghiệm là \(-1\) và \(0\).
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 41 trang 59 Vở bài tập toán 7 tập 2 timdapan.com"







