Giải bài 4 trang 32 vở thực hành Toán 9
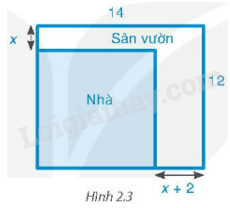
Bác An có một mảnh đất hình chữ nhật có chiều dài 14m và chiều rộng 12m. Bác dự định xây nhà trên mảnh đất đó và dành một diện tích đất để làm sân vườn như hình bên. Biết diện tích đất làm nhà là (100{m^2}). Hỏi x bằng bao nhiêu mét?
Đề bài
Bác An có một mảnh đất hình chữ nhật có chiều dài 14m và chiều rộng 12m. Bác dự định xây nhà trên mảnh đất đó và dành một diện tích đất để làm sân vườn như hình bên. Biết diện tích đất làm nhà là \(100{m^2}\). Hỏi x bằng bao nhiêu mét?
Phương pháp giải - Xem chi tiết
+ Dựa vào dữ kiện đầu bài, lập được phương trình có dạng phương trình tích \(\left( {ax + b} \right)\left( {cx + d} \right) = 0\).
+ Để giải phương trình tích \(\left( {ax + b} \right)\left( {cx + d} \right) = 0\), ta giải hai phương trình \(ax + b = 0\) và \(cx + d = 0\). Sau đó lấy tất cả các nghiệm của chúng.
Lời giải chi tiết
Phần đất làm nhà là một mảnh đất hình chữ nhật có chiều dài và chiều rộng lần lượt là \(14 - x - 2 = 12 - x\left( m \right)\) và \(12 - x\left( m \right)\). Diện tích đất làm nhà là \(\left( {12 - x} \right)\left( {12 - x} \right) = {\left( {12 - x} \right)^2}\;\left( {{m^2}} \right)\)
Ta có: \({\left( {12 - x} \right)^2} = 100\)
\({\left( {12 - x} \right)^2} = {10^2}\)
\({\left( {12 - x} \right)^2} - {10^2} = 0\)
\(\left( {12 - x - 10} \right)\left( {12 - x + 10} \right) = 0\)
\(\left( {2 - x} \right)\left( {22 - x} \right) = 0\)
Giải phương trình trên, kết hợp với điều kiện của x, ta được \(x = 2\).
Search google: "từ khóa + timdapan.com" Ví dụ: "Giải bài 4 trang 32 vở thực hành Toán 9 timdapan.com"







