Bài 39 trang 107 Vở bài tập toán 7 tập 1
Giải bài 39 trang 107 VBT toán 7 tập 1. Xem hình 31. Tại sao Ax//Cy?
Đề bài
Xem hình \(31\).
Tại sao \(Ax//Cy\)?
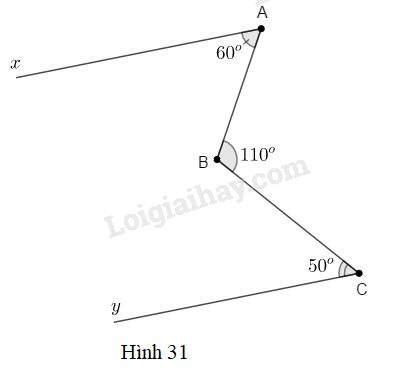
Phương pháp giải - Xem chi tiết
- Định lí : Hai đường thẳng song song với một đường thẳng thì song song với nhau
- Một đường thẳng cắt hai đường thẳng song song với nhau tạo ra cặp góc so le trong bằng nhau, đồng vị bằng nhau, trong cùng phía bù nhau.
- Chứng minh hai đường thẳng song song ta chứng mình cặp góc so le trong (hoặc đồng vị) bằng nhau.
Lời giải chi tiết
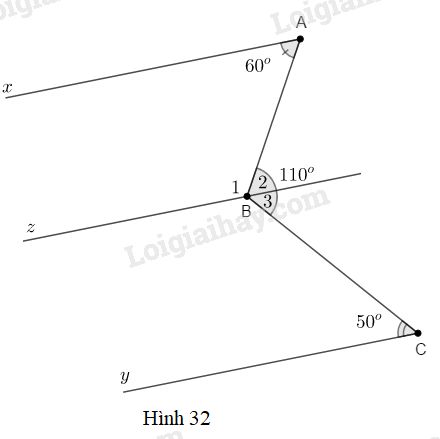
Qua \(B\), vẽ \(Bz//Ax.\)
Theo tính chất về đường thẳng song song, ta có:
\(\widehat {{B_1}} = {180^o} - \widehat A = {180^o} - {60^o} = {120^o}\) (cặp góc trong cùng phía).
\(\widehat {{B_2}} = {180^o} - \widehat {{B_1}} = {180^o} - {120^o} = {60^o}\) (\(\widehat {{B_2}}\) và \(\widehat {{B_1}}\) là hai góc kề bù).
\(\widehat {{B_3}} = \widehat {ABC} - \widehat {{B_2}} = {110^o} - {60^o} = {50^o}\) (giả thiết cho biết \(\widehat {ABC} = {110^o}\)).
Vậy \(\widehat {{B_3}} = \widehat C = {50^o}\) (cặp góc so le trong).
Theo dấu hiệu nhận biết về hai đường thẳng song song, ta có \(Bz/ Cy\).
Do \(Bz//Ax\) (theo cách vẽ) và \(Bz//Cy\) suy ra \(Ax//Cy\) (theo định lí : Hai đường thẳng song song với một đường thẳng thì song song với nhau).
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 39 trang 107 Vở bài tập toán 7 tập 1 timdapan.com"







