Bài 37 trang 106 Vở bài tập toán 7 tập 1
Giải bài 37 trang 106 VBT toán 7 tập 1. Hình 29 cho biết d // d’ // d’’...
Đề bài
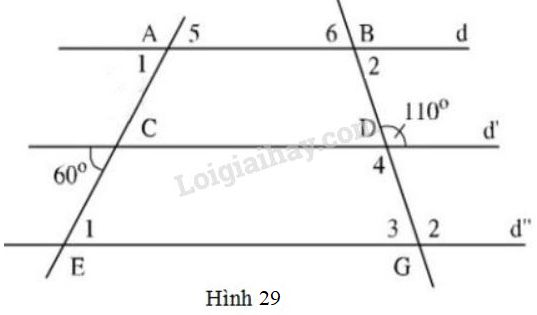
Hình \(29\) cho biết \(d // d’ // d’’\) và hai góc \(60^0 ,110^0\). Tính các góc \(\widehat {E_1},\;\widehat {G_2},\;\widehat {G_3},\; \widehat {D_4},\;\widehat {A_5},\;\widehat {B_6}.\)
Phương pháp giải - Xem chi tiết
- Áp dụng tính chất: nếu một đường thẳng cắt hai đường thẳng song song thì:
a) Hai góc so le trong bằng nhau;
b) Hai góc đồng vị bằng nhau;
c) Hai góc trong cùng phía bù nhau.
- Hai góc đối đỉnh thì bằng nhau.
- Tổng số đo hai góc kề bù bằng \(180^o\).
Lời giải chi tiết
+) Vì \(d’ //d’’\) nên \(\widehat {{E_1}} = 60^o\) (hai góc so le trong).
+) Vì \(d’ // d’’\) nên \(\widehat {{G_2}} = 110^o\) (hai góc đồng vị).
+) \(\widehat {{G_2}} + {\widehat G_3} = {180^o}\) (hai góc kề bù)
\(\Rightarrow \widehat {{G_3}} = {180^o} - \widehat {{G_2}} = {180^o} - {110^o} = {70^o}\)
+) \(\widehat {{D_4}} = 110^o\) (vì hai góc đối đỉnh)
+) Vì \(d //d'\) nên \(\widehat {{A_1}} = 60^o\) (vì hai góc đồng vị)
Ta có: \(\widehat {{A_5}} = \widehat {{A_1}} = 60^o\) (vì hai góc đối đỉnh) .
+ \(\widehat {{B_6}}= \widehat {{B_2}}\) (vì hai góc đối đỉnh)
Có \(\widehat {{B_2}} +110^o=180^o\) (hai góc trong cùng phía)
\( \Rightarrow \widehat {{B_2}} = {180^o} - {110^o} = {70^o}\).
Do đó: \(\widehat {{B_6}}=70^o\).
Vậy \(\widehat {E_1} =60^o,\;\widehat {G_2}= 110^o,\;\widehat {G_3}=70^o,\;\)\( \widehat {D_4} = 110^o,\;\widehat {A_5}= 60^o,\;\widehat {B_6} = 70^o.\)
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 37 trang 106 Vở bài tập toán 7 tập 1 timdapan.com"







