Bài 38 trang 76 Vở bài tập toán 7 tập 1

Đề bài

Hai cạnh của hình chữ nhật có độ dài là \(3\,m\) và \(x\) (m).

Hãy viết công thức biểu diễn diện tích \(y\; ({m^2})\) theo \(x.\)

Vì sao đại lượng \(y\) là hàm số của đại lượng \(x?\)

Hãy vẽ đồ thị của hàm số đó.

Xem đồ thị, hãy cho biết:

a) Diện tích của hình chữ nhật bằng bao nhiêu khi \(x = 3m; x = 4 m?\)

b) Cạnh \(x\) bằng bao nhiêu khi diện tích \(y\) của hình chữ nhật bằng \(6 \,{m^2} ; 9 \,{m^2}?\)

Lời giải chi tiết

Gọi \(y\) là diện tích hình chữ nhật, \(x\) là chiều rộng và chiều dài bằng \(3m\). Vậy ta có: \(y = 3x\).

Từ công thức trên, với mỗi giá trị của \(x\) ta luôn xác định được một giá trị tương ứng của \(y\) nên \(y\) là hàm số của \(x.\)

Vẽ đồ thị (h.12)

Vì đồ thị của hàm số \(y=3x\) là đường thẳng đi qua gốc tọa độ và điểm \(A\).

Cho \(x = 1\) ta có \(y = 3.1=3\).

Vậy đồ thị của hàm số là đường thẳng đi qua \(O(0;0)\) và \(  A(1;3)\).

Xem đồ thị ta thấy:

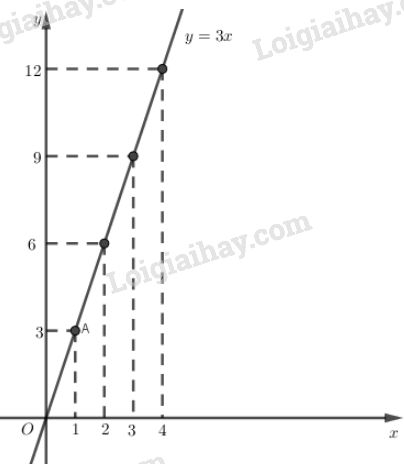
a) Khi \(x = 3\) thì \(  y = 9\). Vậy diện tích hình chữ nhật là: \(9 ({m^2})\)

Khi \(x = 4  \) thì \(  y = 12 .\) Vậy diện tích hình chữ nhật là: \(12 ({m^2})\)

b) Khi \(y = 6 \,m^2\) thì \( x = 2\,m.\)

Khi \(y = 9\,m^2\) thì \( x = 3\,m.\)