Bài 3.43 trang 132 SBT hình học 12
Giải bài 3.43 trang 132 sách bài tập hình học 12. Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng a. Bằng phương pháp tọa độ hãy tính khoảng cách giữa hai đường thẳng CA’ và DD’.
Đề bài
Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng a. Bằng phương pháp tọa độ hãy tính khoảng cách giữa hai đường thẳng CA’ và DD’.
Phương pháp giải - Xem chi tiết
- Chọn hệ trục tọa độ gốc \(C\left( {0;0;0} \right)\) và xác định tọa độ các điểm còn lại.
- Viết phương trình mặt phẳng chứa \(CA'\) và song song \(DD'\).
- Tính khoảng cách \(d\left( {CA',DD'} \right) = d\left( {DD',\left( \alpha \right)} \right) = d\left( {D,\left( \alpha \right)} \right)\)
Lời giải chi tiết
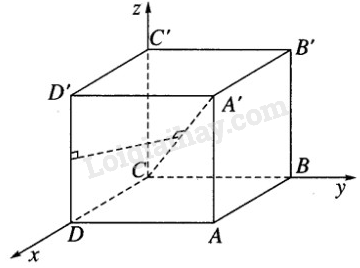
Ta chọn hệ trục tọa độ sao cho: C là gốc tọa độ, \(\overrightarrow {CD} = a\overrightarrow i ;\overrightarrow {CB} = a\overrightarrow j ;\overrightarrow {CC'} = a\overrightarrow k \)
Trong hệ tọa độ vừa chọn ta có: C(0; 0; 0), A’(a; a ; a), D(a,; 0;0), D’(a; 0; a)
\(\overrightarrow {CA'} = (a;a;a),\overrightarrow {{\rm{DD}}'} = (0;0;a)\)
Gọi \((\alpha )\) là mặt phẳng chứa \(\overrightarrow {CA'} \) và song song với \(\overrightarrow {DD'} \).
Mặt phẳng \((\alpha )\) có vecto pháp tuyến là: \(\overrightarrow n = \left[ {\overrightarrow {CA'} ,\overrightarrow {{\rm{DD}}'} } \right] = ({a^2}; - {a^2};0)\) hay x – y = 0
Phương trình tổng quát của \((\alpha )\) là x – y = 0.
Ta có: \(d\left( {CA',DD'} \right) = d\left( {D,\left( \alpha \right)} \right)\) \( = \dfrac{{\left| { - a} \right|}}{{\sqrt {1 + 1 + 0} }} = \dfrac{a}{{\sqrt 2 }}\).
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 3.43 trang 132 SBT hình học 12 timdapan.com"







