Bài 3.32 trang 130 SBT hình học 12
Giải bài 3.32 trang 130 sách bài tập hình học 12. Viết phương trình của đường thẳng nằm trong mặt phẳng ...
Đề bài
Viết phương trình của đường thẳng \(\Delta \) nằm trong mặt phẳng \((\alpha )\): x + 2z = 0 và cắt hai đường kính \({d_1}:\left\{ {\begin{array}{*{20}{c}}{x = 1 - t}\\{y = t}\\{z = 4t}\end{array}} \right.\) và \({d_2}:\left\{ {\begin{array}{*{20}{c}}{x = 2 - t'}\\{y = 4 + 2t'}\\{z = 4}\end{array}} \right.\)
Phương pháp giải - Xem chi tiết
- Tham số hóa tọa độ hai giao điểm.
- Thay tọa các điểm vào phương trình mặt phẳng \(\left( \alpha \right)\), từ đó suy ra tọa độ các điểm.
- Viết phương trình đường thẳng đi qua hai điểm và kết luận.
Lời giải chi tiết
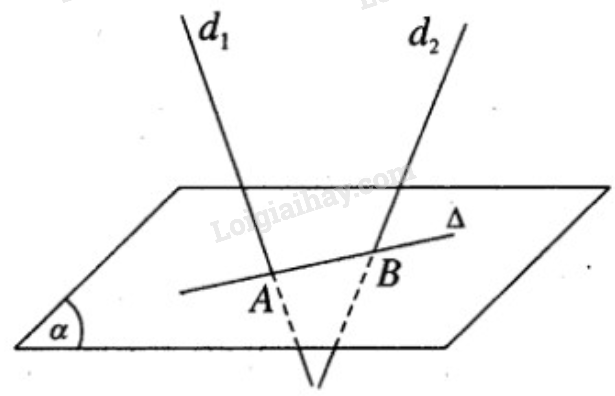
Gọi A và B lần lượt là giao điểm của \({d_1}\) và \({d_2}\) với \((\alpha )\).
Đường thẳng \(\Delta \) cần tìm chính là đường thẳng AB.
Ta có: \(A(1 - t;t;4t) \in {d_1}\)
\(A \in (\alpha ) \Leftrightarrow t + 4.(2t) = 0 \Leftrightarrow t = 0\)
Suy ra: A(1; 0; 0)
Ta có : \(B(2 - t';4 + 2t';4) \in {d_2}\)
\(B \in (\alpha ) \Leftrightarrow 4 + 2t' + 8 = 0 \Leftrightarrow t' = - 6\)
Suy ra B(8; -8; 4)
\(\Delta \) đi qua A, B nên có vecto chỉ phương \(\overrightarrow {{u_\Delta }} = \overrightarrow {AB} = (7; - 8;4)\)
Phương trình chính tắc của \(\Delta \) là: \(\dfrac{{x - 1}}{7} = \dfrac{y}{{ - 8}} = \dfrac{z}{4}\)
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 3.32 trang 130 SBT hình học 12 timdapan.com"







