Bài 31 trang 91 SBT toán 6 tập 2

Đề bài

a) Vẽ góc bẹt \(xOy\).

b) Vẽ tia \(Ot\) sao cho \(\widehat {xOt} = {30^o}\)

c) Vẽ tia \(Oz\) sao cho \(\widehat {y{\rm{O}}z} = {30^o}\)  (\(Ot\) và \(Oz\) cùng nằm trên một nửa mặt phẳng bờ \(xy\))

d) Vẽ tia phân giác \(Om\) của góc \(tOz\);

e) Vì sao tia \(Om\) cũng là tia phân giác của \(\widehat {xOy}\) ?

Lời giải chi tiết

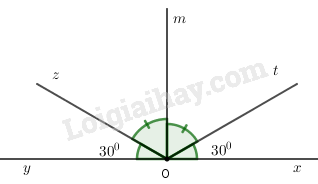
a) Ta có hình vẽ các câu a, b, c, d : 

e) Vì \(\widehat {xOt}\) và \(\widehat {tOy}\) kề bù nên: \(\widehat {xOt} + \widehat {tOy} = {180^o}\)

Thay \(\widehat {xOt} = {30^o}\) ta có :

\({30^o} + \widehat {tOy} = {180^o}\) 

\( \Rightarrow \widehat {tOy} = {180^o} - {30^o} = {150^o}\)

Vì \(Oz\) và \(Ot\) nằm trên nửa mặt phẳng bờ chứa tia \(Oy\) và \(\widehat {xOz} < \widehat {y{\rm{O}}t}\) nên tia \(Oz\) nằm giữa tia \(Oy\) và \(Ot\)

\( \Rightarrow \widehat {y{{O}}z} + \widehat {zOt} = \widehat {y{{O}}t}\)

\(\Rightarrow \widehat {zOt} = \widehat {y{{O}}t} - \widehat {y{{O}}z}\)

\( \Rightarrow \widehat {zOt} = {150^o} - {30^o} = {120^o}\)

Vì tia \(Om\) là tia phân giác \(\widehat {tOz}\) nên \(\displaystyle \widehat {tOm} = \widehat {mOz} = {{\widehat {tOz}} \over 2} = {60^o}\)

Vì \(Ot\) nằm giữa  \(Ox\) và \(Om\) nên \(\widehat {xOt} + \widehat {tOm} = \widehat {xOm}\) 

\( \Rightarrow \widehat {xOm} = {30^o} + {60^o} = {90^o}\). 

Vậy \(Om\) là tia phân giác \(\widehat {xOy}\).