Bài 29 trang 83 SBT toán 8 tập 1
Giải bài 29 trang 8 sách bài tập toán 8. Hai đoạn thẳng AB và CD cắt nhau tại O. Biết rằng OA = OC, OB = OD. Tứ giác ACBD là hình gì ? Vì sao ?
Đề bài
Hai đoạn thẳng \(AB\) và \(CD\) cắt nhau tại \(O.\) Biết rằng \(OA = OC,\) \(OB = OD.\) Tứ giác \(ACBD\) là hình gì \(?\) Vì sao \(?\)
Phương pháp giải - Xem chi tiết
Ta sử dụng kiến thức:
+) Hình thang là tứ giác có hai cạnh đối song song.
+) Hình thang có hai đường chéo bằng nhau là hình thang cân.
Lời giải chi tiết
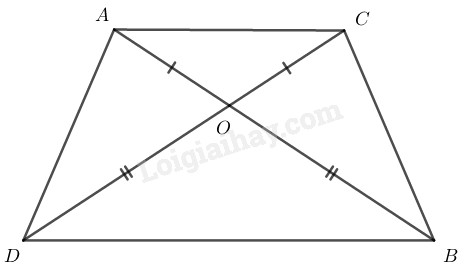
Ta có: \(OA = OC \;\;\;(gt)\)
\(⇒ ∆ OAC\) cân tại \(O\)
\( \Rightarrow {\widehat {OAC}} =\displaystyle {{{{180}^0} - \widehat {AOC}} \over 2}\) (tính chất tam giác cân) \((1)\)
\(OB = OD \;\;\;(gt)\)
\(⇒ ∆ OBD\) cân tại \(O\)
\( \Rightarrow {\widehat {OBD}} = \displaystyle {{{{180}^0} - \widehat {BOD}} \over 2}\) (tính chất tam giác cân) \((2)\)
\(\widehat {AOC} = \widehat {BOD}\) (đối đỉnh) \((3)\)
Từ \((1),\) \((2)\) và \((3)\) suy ra: \({\widehat {OAC}} = {\widehat {OBD}}\)
\(⇒ AC // BD\) (vì có cặp góc ở vị trí so le trong bằng nhau)
Suy ra: Tứ giác \(ACBD\) là hình thang
Ta có: \(AB = OA + OB\)
\( CD = OC + OD\)
Mà \(OA = OC,\) \(OB = OD\)
Suy ra: \(AB = CD\)
Vậy hình thang \(ACBD\) là hình thang cân.
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 29 trang 83 SBT toán 8 tập 1 timdapan.com"







