Bài 29 trang 55 SBT toán 9 tập 2
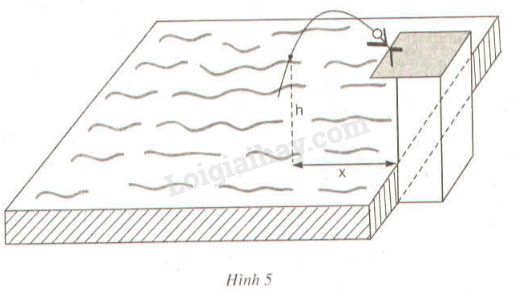
Giải bài 29 trang 55 sách bài tập toán 9. Một vận động viên bơi lội nhảy cầu (xem hình 5). Khi nhảy, độ cao h từ người đó tới mặt nước (tính bằng mét) phụ thuộc vào khoảng cách x từ điểm rơi đến chân cầu (tính bằng mét)
Một vận động viên bơi lội nhảy cầu (xem hình 5). Khi nhảy, độ cao h từ người đó tới mặt nước (tính bằng mét) phụ thuộc vào khoảng cách \(x\) từ điểm rơi đến chân cầu (tính bằng mét) bởi công thức:
\(h = - {\left( {x - 1} \right)^2} + 4\)
Hỏi khoảng cách x bằng bao nhiêu:
LG a
Khi vận động viên ở độ cao \(3m\)?
Phương pháp giải:
Thay \(h=3m\) vào phương trình \(h = - {\left( {x - 1} \right)^2} + 4\), từ đó ta tìm \(x\).
Lời giải chi tiết:
Khi \(h = 3m\) ta có:
\(\eqalign{
& 3 = - {\left( {x - 1} \right)^2} + 4 \cr&\Leftrightarrow {\left( {x - 1} \right)^2} - 1 = 0 \cr
& \Leftrightarrow {x^2} - 2x + 1 - 1 = 0\cr& \Leftrightarrow x\left( {x - 2} \right) = 0\cr& \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = 2\end{array} \right.\cr} \)
Vậy \(x = 0\, m\) hoặc \(x = 2\,m\).
LG b
Khi vận động viên chạm mặt nước?
Phương pháp giải:
Khi chạm mặt nước ta có \(h=0\), thay \(h=0\) vào phương trình \(h = - {\left( {x - 1} \right)^2} + 4\) từ đó ta tìm \(x\).
* Phương trình \(a{x^2} + bx + c = 0\,(a \ne 0)\) và \(b = 2b'\), \(\Delta ' = b{'^2} - ac\)
+ Nếu \(\Delta ' >0\) thì phương trình có hai nghiệm phân biệt:
\({x_1}=\dfrac{-b' + \sqrt{\bigtriangleup '}}{a}\); \({x_2}=\dfrac{-b' - \sqrt{\bigtriangleup '}}{a}\)
+ Nếu \(\Delta ' =0\) thì phương trình có nghiệm kép \({x_1}={x_2}=\dfrac{-b'}{a}\).
+ Nếu \(\Delta ' <0\) thì phương trình vô nghiệm.
Lời giải chi tiết:
Khi vận động viên chạm mặt nước ta có \(h = 0\).
\(\eqalign{
& \Leftrightarrow - {\left( {x - 1} \right)^2} + 4 = 0\cr& \Leftrightarrow {\left( {x - 1} \right)^2} - 4 = 0\cr& \Leftrightarrow {x^2} - 2x +1- 4 = 0\cr& \Leftrightarrow {x^2} - 2x - 3 = 0 \cr
& \Delta ' = b{'^2} - ac= {\left( { - 1} \right)^2} - 1.\left( { - 3} \right) = 4 > 0 \cr
& \sqrt {\Delta '} = \sqrt 4 = 2 \cr
& {x_1} =\dfrac{-b' + \sqrt{\bigtriangleup '}}{a}= {{1 + 2} \over 1} = 3 \cr
& {x_2} =\dfrac{-b' - \sqrt{\bigtriangleup '}}{a}= {{1 - 2} \over 1} = - 1 \cr} \)
Vì khoảng cách không âm nên \(x = 3\,m\).
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 29 trang 55 SBT toán 9 tập 2 timdapan.com"







