Bài 28 trang 104 Vở bài tập toán 9 tập 2

Đề bài

Cho đường tròn \((O)\) và hai dây cung song song \(AB, CD\) (\(A\) và \(C\) nằm trong cùng một mặt phẳng bờ \(BD\)) ; \(AD\) cắt \(BC\) tại \(I\). Chứng minh rằng \(\widehat {AOC} = \widehat {AIC}\).

Lời giải chi tiết

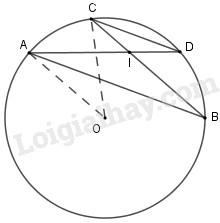
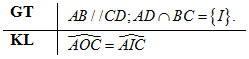
Góc \(\widehat {AOC}\) là góc ở tâm chắn cung \(AC\)

Nên ta có : \(\widehat {AOC} = \) sđ\(\overparen{AC}\)               (1)

Góc \(AIC\) là góc có đỉnh ở bên trong đường tròn nên ta có :

                \(\widehat {AIC} = \dfrac{1}{2}\)(sđ\(\overparen{AC}+\) sđ\(\overparen{BD}\))         (2)

Vì \(AB//CD \Rightarrow \) \(\overparen{AC} =\overparen{BD}\)            (3)

Vậy từ (1) , (2) và (3) ta có \(\widehat {AOC} = \widehat {AIC}\)

Nhận xét : Trong quá trình giải bài toán chứng minh các góc bằng nhau, ta sử dụng các khái niệm về số đo của góc tương ứng, định lí và hệ quả của nó; đồng thời áp dụng tính chất đồng dạng của tam giác để chứng minh tỉ số hai đoạn thẳng.