Bài 23 trang 101 Vở bài tập toán 9 tập 2

Đề bài

Cho đường tròn \((O)\) và hai dây \(AB, AC\). Gọi \(M, N\) lần lượt là điểm chính giữa của cung \(AB\) và cung \(AC\). Đường thẳng \(MN\) cắt dây \(AB\) tại \(E\) và cắt dây \(AC\) tại \(H\). Chứng minh tam giác \(AEH\) là tam giác cân.

Lời giải chi tiết

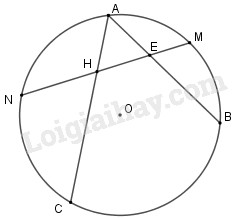
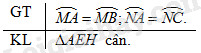
Xét \(\Delta AEH\), ta có :

(1)           \(\widehat {AEN} = \dfrac{1}{2}\)(sđ\(\overparen{MB}\)+ sđ\(\overparen{AN}\));

(2)           \(\widehat {AHM} = \dfrac{1}{2}\)(sđ\(\overparen{MA}\)+ sđ\(\overparen{CN}\))

Vì (1) và (2) là các góc có đỉnh bên trong đường tròn.

Theo giả thiết ta có \(\overparen{MB}=\overparen{MB}\); \(\overparen{NA}=\overparen{NC}\)

Vậy từ (1) và (2) ta có \(\widehat {AEN} = \widehat {AHM} \Rightarrow \Delta AEH\) cân tại \(A.\)