Bài 25 trang 102 Vở bài tập toán 9 tập 2

Đề bài

Trên một đường tròn, lấy liên tiếp ba cung \(AC,CD,DB\) sao cho sđ\(\overparen{AC}\) =sđ\(\overparen{CD}\) =sđ \(\overparen{DB} = 60^\circ \) . Hai đường thẳng \(AC\) và \(BD\) cắt nhau tại \(E\). Hai tiếp tuyến của đường tròn tại \(B\) và \(C\) cắt nhau tại \(T\).

 Chứng minh rằng :

a) \(\widehat {AEB} = \widehat {BTC}\) ;

b) CD là tia phân giác của \(\widehat {BTC}\).

Lời giải chi tiết

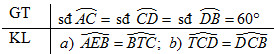
a) Xét hai góc \(AEB\) và \(BTC,\) ta có \(E,T\) nằm ngoài đường tròn nên

 \(\widehat {AEB} = \dfrac{1}{2}\)(\(sđ \,\overparen{AB}\) - \(sđ \,\overparen{CD}\)) \( = \dfrac{1}{2}\left( {180^\circ  - 60^\circ } \right) = 60^\circ \).

\(\widehat {BTC} = \dfrac{1}{2}{\rm{[}}(\)\(sđ \,\overparen{AB}+sđ \,\overparen{AC}\))  \(-(sđ \,\overparen{CD}+sđ \,\overparen{DB}\)\(){\rm{]}}\)

Từ giả thiết ta có \(sđ \,\overparen{AC}=sđ \,\overparen{CD}\) \(=sđ \,\overparen{DB} = 60^\circ \) và \(sđ \,\overparen{AB}\) \(=sđ \,\overparen{AC}+sđ \,\overparen{CD}+sđ \,\overparen{DB}\) \( = 180^\circ \)

Vậy \(\widehat {AEB} = \widehat {BTC}\) (đpcm).

b)  Ta có \(\widehat {DCB} = \dfrac{1}{2}\) sđ\(\overparen{BD}\)\( = 30^\circ \)(góc nội tiếp chắn cung \(BD\));

\(\widehat {DCT} = \dfrac{1}{2}\)sđ\(\overparen{CD}\)\( = 30^\circ \) (vì góc tạo bởi tia tiếp tuyến và dây cung \(DC\))

Theo giả thiết \(\overparen{CD}=\overparen{DB}\) 

nên \(\widehat {DCB} = \widehat {DCT} \Rightarrow \) \(CD\) là tia phân giác của \(\widehat {BCT}\) (đpcm) .