Bài 2.3 trang 47 SBT hình học 12

Đề bài

Cho \(S.ABC\) là hình chóp tam giác đều có các cạnh bên bằng \(a\) và có góc giữa các mặt bên và mặt phẳng đáy là \(\alpha \). Hình nón đỉnh \(S\) có đường tròn đáy nội tiếp tam giác đều \(ABC\) gọi là hình nón nội tiếp hình chóp đã cho. Hãy tính diện tích xung quanh của hình nón này theo \(a \) và \(\alpha \).

Lời giải chi tiết

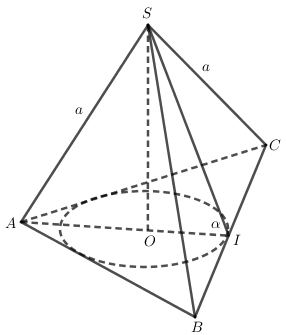
Gọi \(I\) là trung điểm của cạnh \(BC\) và \(O\) là tâm của tam giác đều \(ABC\).

Theo giả thiết ta có \(SA = SB = SC = a \) và \(\widehat {SIO} = \alpha \).

Đặt \(OI = r, SO = h\), ta có \(AO = 2r\) và \(\left\{ {\begin{array}{*{20}{c}}{h = r\tan \alpha }\\{{a^2} = {h^2} + 4{r^2}}\end{array}} \right.\)    (vì \(S{A^2} = {\rm{ }}S{O^2} + {\rm{ }}A{O^2}\))

Do đó \({a^2} = {r^2}{\tan ^2}\alpha  + 4{r^2} = {r^2}({\tan ^2}\alpha  + 4)\)

Vậy \(r = \dfrac{a}{{\sqrt {{{\tan }^2}\alpha  + 4} }}\)

Hình nón nội tiếp có đường sinh là: \(l = SI = \dfrac{r}{{\cos \alpha }} = \dfrac{a}{{\cos \alpha \sqrt {{{\tan }^2}\alpha  + 4} }}\)

Diện tích xung quanh của hình nón nội tiếp hình chóp \(S.ABC\) là:

\({S_{xq}} = \pi rl\)\( = \pi .\dfrac{a}{{\sqrt {{{\tan }^2}\alpha  + 4} }}.\dfrac{a}{{\cos \alpha \sqrt {{{\tan }^2}\alpha  + 4} }}\) \( = \dfrac{{\pi {a^2}}}{{\cos \alpha ({{\tan }^2}\alpha  + 4)}}\)