Bài 2.26 trang 62 SBT hình học 12

Đề bài

Cho hình chóp S.ABC và biết rằng có một mặt cầu tiếp xúc với tất cả các cạnh bên của hình chóp đồng thời tiếp xúc với ba cạnh của đáy tại trung điểm của mỗi cạnh đáy. Chứng minh hình chóp đó là hình chóp đều.

Lời giải chi tiết

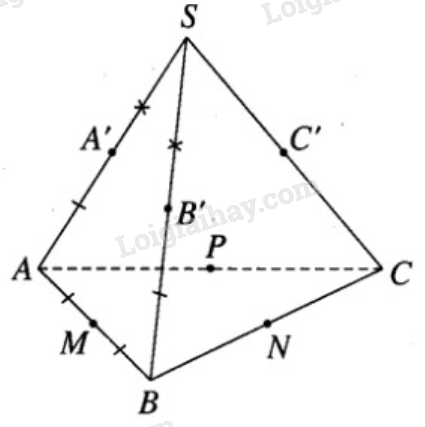
Gọi M, N, P lần lượt là trung điểm của các cạnh AB, BC, CA và A’ , B’, C’ là các điểm tiếp xúc của các cạnh bên SA, SB, SC với mặt cầu. Ta có AA’ và AM là hai tiếp tuyến nên AM = AA’. Vì M là trung điểm của AB nên AM = MB.

Mặt khác BM = BB’, ta suy ra AA’ = BB’

Vì SA’ = SB’ nên SA’ + A’A = SB’ + B’B  hay SA = SB.

Tương tự, ta chứng minh được SB = SC

Do đó SA = SB = SC.

Mặt khác AB = 2BM = 2BN = BC = 2CN=2CP = CA

Vậy AB = BC = CA và ABC là một tam giác đều nên là một hình chóp đều. Ta có đường cao kẻ từ S có chân H là tâm đường tròn ngoại tiếp tam giác đều ABC.