Bài 22 trang 100 Vở bài tập toán 9 tập 2
Giải bài 22 trang 100 VBT toán 9 tập 2. Cho đường tròn (O) và điểm M nằm bên ngoài đường tròn đó. Qua điểm M kẻ tiếp tuyến MT và cắt MAB...
Đề bài
Cho đường tròn (O) và điểm M nằm bên ngoài đường tròn đó. Qua điểm M kẻ tiếp tuyến MT và cắt MAB. Chứng minh MT2 = MA.MB.
Phương pháp giải - Xem chi tiết
+ Sử dụng hệ quả: Trong một đường tròn, góc tạo bởi tia tiếp tuyến và dây cung và góc nội tiếp cùng chắn một cung thì bằng nhau.
+ Chứng minh \(\Delta {\rm M}{\rm T}{\rm A} \backsim \Delta {\rm M}{\rm B}{\rm T}\) để suy ra đẳng thức cần chứng minh.
Lời giải chi tiết
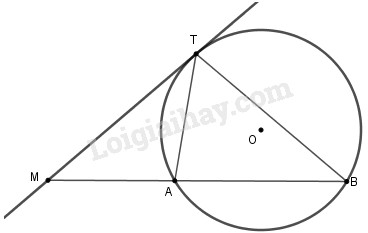
Xét \(\Delta MTA\) và \(\Delta MBT\) có \(\widehat {MTA} = \widehat {ABT}\) (do \(\widehat {MTA}\) là góc tạo bởi tiếp tuyến \(MT\) và dây cung \(AT\); \(\widehat {ABT}\) là góc nội tiếp chắn cung \(AT\)) và \(\widehat M\) chung Vậy \(\Delta MTA \backsim \Delta MBT\left( {g - g} \right)\)
Suy ra \(\dfrac{{MT}}{{MB}} = \dfrac{{MA}}{{MT}} \Leftrightarrow M{T^2} = MA.MB\) (đpcm)
Nhận xét: Đoạn thẳng MT được gọi là trung bình nhân của hai đoạn MA và MB.
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 22 trang 100 Vở bài tập toán 9 tập 2 timdapan.com"







