Bài 2.14 trang 36 SBT đại số 10

LG a

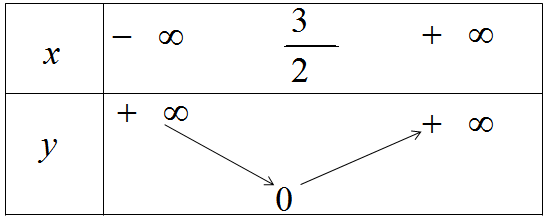
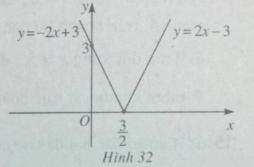
\(y = |2x - 3|\);

Phương pháp giải:

Sử dụng kiến thức về giá trị tuyệt đối và cách vẽ bảng biến thiên.

Lời giải chi tiết:

 Ta có thể viết

\(y = \left\{ \begin{array}{l}2x - 3,x \ge \dfrac{3}{2}\\ - 2x + 3,x < \dfrac{3}{2}\end{array} \right.\)

Từ đó có bảng biến thiên và đồ thị của hàm số \(y = |2x - 3|\)(h.32)

LG b

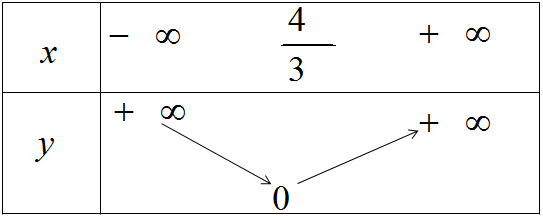
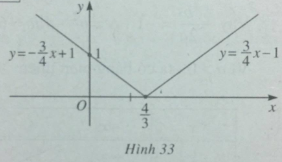
\(y = | - \dfrac{3}{4}x + 1|\)

Phương pháp giải:

Sử dụng kiến thức về giá trị tuyệt đối và cách vẽ bảng biến thiên.

Lời giải chi tiết:

Ta có thể viết

\(y = \left\{ \begin{array}{l} - \dfrac{3}{4}x + 1,x \le \dfrac{4}{3}\\\dfrac{3}{4}x - 1,x > \dfrac{4}{3}\end{array} \right.\)

Bảng biến thiên và đồ thị của hàm số \(y = | - \dfrac{3}{4}x + 1|\)(h.33)

LG c

\(y = x + |x|\).

Phương pháp giải:

Sử dụng kiến thức về giá trị tuyệt đối và cách vẽ bảng biến thiên.

Lời giải chi tiết:

Với \(x \ge 0\) thì \(y = x + \left| x \right| = x + x = 2x\)

Với \(x < 0\) thì \(y = x + \left| x \right| = x - x = 0\)

Do đó ta có thể viết \(y = \left\{ \begin{array}{l}0,x < 0\\2x,x \ge 0\end{array} \right.\)

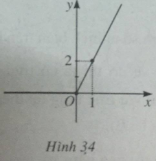
Đồ thị của hàm số \(y = x + |x|\)được vẽ trên hình 34.