Giải bài 2 trang 92 sách bài tập toán 9 - Chân trời sáng tạo tập 1

Đề bài

Cho đường tròn (O; R) và dây cung MN = \(R\sqrt 3 \). Tính số đo của mỗi cung \(\overset\frown{MN}\) (cung lớn và cung nhỏ).

Lời giải chi tiết

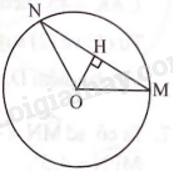
Kẻ \(OH \bot MN\)tại H. Ta có OM = ON = R, suy ra tam giác OMN cân tại O, suy ra HM = HN.

Dó đó HM = HN = \(\frac{{MN}}{2} = \frac{{R\sqrt 3 }}{2}\).

Ta có: \(cos\widehat {HMO} = \frac{{HM}}{2} = \frac{{\frac{{R\sqrt 3 }}{2}}}{R} = \frac{{\sqrt 3 }}{2},\)

Nên \(\widehat {HMO} = {30^o}\), suy ra \(\widehat {MON} = {120^o}\).

Suy ra số đo cung nhỏ \(\overset\frown{MN}\) là 120^o, số đo cung lớn \(\overset\frown{MN}\) = 360^o – 120^o = 240^o.