Giải bài 2 trang 72 SGK Toán 7 tập 2 - Chân trời sáng tạo
Cho tam giác nhọn ABC. Gọi M, N, P lần lượt là trung điểm của các cạnh AB, BC, CA và cho O là điểm cách đều ba đỉnh của tam giác ABC. Chứng minh rằng MO vuông góc với AB, NO vuông góc với BC, PO vuông góc với AC.
Đề bài
Cho tam giác nhọn ABC. Gọi M, N, P lần lượt là trung điểm của các cạnh AB, BC, CA và cho O là điểm cách đều ba đỉnh của tam giác ABC. Chứng minh rằng MO vuông góc với AB, NO vuông góc với BC, PO vuông góc với AC.
Phương pháp giải - Xem chi tiết
Ta chứng minh OM, ON, OP là các đường trung trực tương ứng với cạnh của tam giác
Lời giải chi tiết
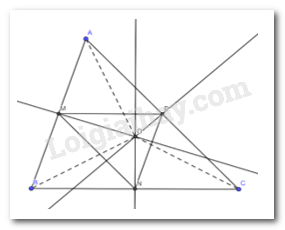
Theo giả thiết ta có :
OA = OB, MA = MB ( do M là trung điểm AB )
\( \Rightarrow \) MO là đường trung trực của đoạn thẳng AB
\( \Rightarrow \) MO vuông góc với AB
Theo giả thiết ta có :
OA = OC, PC = PA ( do P là trung điểm AC )
\( \Rightarrow \) PO là đường trung trực của đoạn thẳng AC
\( \Rightarrow \) PO vuông góc với AC
Theo giả thiết ta có :
OC = OB, NC = NB ( do N là trung điểm BC )
\( \Rightarrow \) NO là đường trung trực của đoạn thẳng BC
\( \Rightarrow \) NO vuông góc với BC
Search google: "từ khóa + timdapan.com" Ví dụ: "Giải bài 2 trang 72 SGK Toán 7 tập 2 - Chân trời sáng tạo timdapan.com"







