Bài 160 trang 100 SBT Toán 8 tập 1

Đề bài

Cho tứ giác ABCD. Gọi E, F, G, H theo thứ tự là trung điểm của AB, AC, DC, DB. Tìm điều kiện của tứ giác ABCD để EFGH là:

a. Hình chữ nhật

b. Hình thoi

c. Hình vuông

Lời giải chi tiết

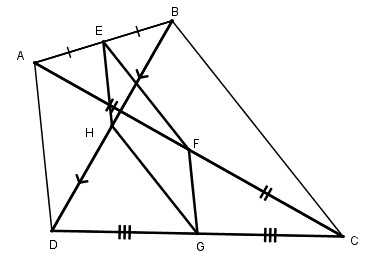
Xét tam giác ABC: 

Ta có: EB = EA, FA = FC (gt)

Nên EF là đường trung bình của tam giác ABC

Suy ra EF // BC, EF = \(\displaystyle {1 \over 2}\)  BC (tính chất)

Xét tam giác BDC có: 

HB = HD, GD = GC (gt)

Nên HG là đường trung bình của tam giác BDC

Suy ra HG // BC, HG =  \(\displaystyle {1 \over 2}\)  BC (tính chất) 

Do đó EF //HG, EF = HG.

Vậy EFGH là hình bình hành.

Xét tam giác ABD: 

Ta có: EB = EA, HB = HD (gt)

Nên EH là đường trung bình của tam giác ABD

Suy ra EH // AD, EH = \(\displaystyle {1 \over 2}AD\) (tính chất)

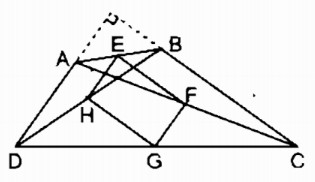
a) Hình bình hành EFGH là hình chữ nhật ⇔ EH ⊥ EF

Mà EF // BC và EH//AD (chứng minh trên)

Do đó \(EH ⊥ EF⇔ AD ⊥ BC \)

Hay để EFGH là hình chữ nhật thì \(AD ⊥ BC \)

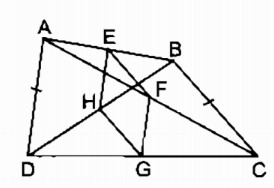
b) Hình bình hành EFGH là hình thoi ⇔ EH = EF

Mà EH = \(\displaystyle {1 \over 2}AD\) và EF = \(\displaystyle {1 \over 2}\)  BC (chứng minh trên)

Nên \(EH = EF⇔ AD = BC\)

Vậy EFGH là hình thoi ⇔ AD = BC. 

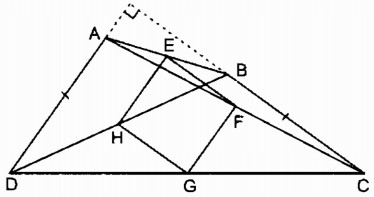
c)  EFGH là hình vuông khi EFGH vừa là hình thoi, vừa là hình chữ nhật

Từ câu a, b ta có EFGH là hình vuông ⇔ AD ⊥ BC và AD = BC