Bài 156 trang 99 SBT Toán 8 tập 1
Giải bài 156 trang 99 sách bài tập toán 8. Cho hình vuông ABCD. Vẽ điểm E trong hình vuông sao cho góc EDC bằng góc ECD và bằng 15 độ. a. Vẽ điểm F trong hình vuông sao cho góc FAD bằng góc FDA và bằng...
Đề bài
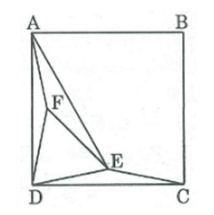
Cho hình vuông ABCD. Vẽ điểm E trong hình vuông sao cho \(\widehat {EDC} = \widehat {ECD} = {15^0}\).
a. Vẽ điểm F trong hình vuông sao cho \(\widehat {FAD} = \widehat {FDA} = {15^0}\). Chứng minh rằng tam giác DEF là tam giác đều.
b. Chứng minh rằng tam giác ABE là tam giác đều.
Phương pháp giải - Xem chi tiết
Vận dụng tính chất của hai tam giác bằng nhau và tính chất về các cạnh và góc của hình vuông.
Lời giải chi tiết
a. Xét \(∆ EDC\) và \(∆ FDA :\)
\(\widehat {EDC} = \widehat {FAD} = {15^0}\)
\(DC = AD\) (do ABCD là hình vuông)
\(\widehat {ECD} = \widehat {FDA} = {15^0}\)
Do đó: \(∆ EDC = ∆ FDA\) (g.c.g)
\(⇒ DE = DF\)
\(⇒ ∆ DEF\) cân tại D
Ta lại có:
\( \widehat {ADC} = \widehat {FDA} + \widehat {FDE} + \widehat {EDC} \)\( \Rightarrow \widehat {FDE} = \widehat {ADC} - \left( {\widehat {FDA} + \widehat {EDC}} \right) \)\( = {90^0} - \left( {{{15}^0} + {{15}^0}} \right) = {60^0} \)
Vậy \(∆ DEF\) đều.
b. Vì \(\widehat {ECD} = {15^0}\) và \(\widehat {DCB} = {90^0}\) nên \(\widehat {ECB} = 90^0-{15^0}=75^0\)
Vì \(\widehat {FDA} = {15^0}\) và \(\widehat {FDE} = {60^0}\) (do tam giác FDE đều) nên \(\widehat {EDA} = 60^0+{15^0}=75^0\)
Xét \(∆ ADE\) và \(∆ BCE:\)
\(ED = EC\) (vì \(∆ EDC\) cân tại E)
\(\widehat {ADE} = \widehat {BCE} = {75^0}\)
\(AD = BC\) (do ABCD là hình vuông)
Do đó: \(∆ ADE = ∆ BCE\) (c.g.c)
\(⇒ AE = BE\) (1)
Trong \(∆ AFD\) ta có:
\(\widehat {AFD} = {180^0} - \left( {\widehat {FAD} + \widehat {FDA}} \right) \)\(= {180^0} - \left( {{{15}^0} + {{15}^0}} \right) = {150^0} \)
\( \widehat {AFD} + \widehat {DFE} + \widehat {AFE} = {360^0} \)\( \Rightarrow \widehat {AFE} = {360^0} - \left( {\widehat {AFD} + \widehat {DFE}} \right) \)\( = {360^0} - \left( {{{150}^0} + {{60}^0}} \right) \)\(= {150^0} \)
Xét \(∆ AFD\) và \(∆ AEF:\)
\(AF\) cạnh chung
\(\widehat {AFD} = \widehat {AFE} = {150^0}\)
\(DF = EF\) (vì \(∆ DFE\) đều)
Do đó: \(∆ AFD = ∆ AEF\) (c.g.c)
\(⇒ AE = AD\)
\(AD = AB\) (do ABCD là hình vuông)
Suy ra: \(AE = AB\) (2)
Từ (1) và (2) suy ra: \(AE = AB = BE.\)
Vậy \(∆ AEB\) đều.
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 156 trang 99 SBT Toán 8 tập 1 timdapan.com"