Bài 144 trang 98 SBT Toán 8 tập 1
Giải bài 144 trang 98 sách bài tập toán 8. Cho tam giác ABC vuông tại A, đường phân giác AD. Gọi M, N theo thứ tự là chân các đường vuông góc kẻ từ D đến AB, AC. Chứng minh rằng tứ giác AMDN là hình vuông...
Đề bài
Cho tam giác \(ABC\) vuông tại \(A,\) đường phân giác \(AD.\) Gọi \(M,\, N\) theo thứ tự là chân các đường vuông góc kẻ từ \(D\) đến \(AB,\, AC.\) Chứng minh rằng tứ giác \(AMDN\) là hình vuông.
Phương pháp giải - Xem chi tiết
Vận dụng các dấu hiệu nhận biết hình vuông để chứng minh.
Tứ giác có 3 góc vuông là hình chữ nhật
Hình chữ nhật có đường chéo là phân giác của 1 góc là hình vuông.
Lời giải chi tiết
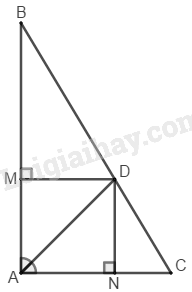
Xét tứ giác \(AMDN:\)
\(\widehat {MAN} ={90^o} \) (gt)
\(DM ⊥ AB\) (gt)
\( \Rightarrow \widehat {AMD}={90^o}\)
\(DN ⊥ AC\) (gt)
\( \Rightarrow \widehat {AND}={90^o}\)
Suy ra: Tứ giác \(AMDN\) là hình chữ nhật (vì có ba góc vuông), có đường chéo \(AD\) là đường phân giác của góc \(A.\)
Vậy: Hình chữ nhật \(AMDN\) là hình vuông.
Mẹo Tìm đáp án nhanh nhất
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 144 trang 98 SBT Toán 8 tập 1 timdapan.com"
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 144 trang 98 SBT Toán 8 tập 1 timdapan.com"







