Bài 15.13* trang 44 SBT Vật Lí 12

Đề bài

Mạch điện xoay chiều gồm một điện trở, một cuộn dây và một tụ điện ghép nối tiếp (\(H.15.2).\) Điện áp tức thời giữa hai đầu đoạn mạch \(u = 65\sqrt 2 cos100\pi t(V).\)

Các điện áp hiệu dụng \({U_{AM}} = 13V;{U_{MN}} = 13V;{U_{NB}} = 65V.\)

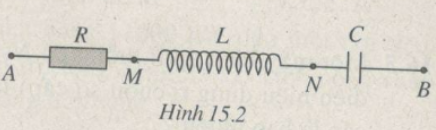
a) Chứng tỏ rằng cuộn dây có điện trở thuần \(r \ne 0.\)

b) Tính hệ số công suất của mạch.

Lời giải chi tiết

a) Xét \(U_{AM}^2 + {({U_{MN}} - {U_{NB}})^2} \\= {13^2} + {(13 - 65)^2} = 2873\)

\(U_{AB}^2 = {65^2} = 4225\)

Nhận thấy \(U_{AB}^2 \ne {U_{AM}}^2 + {({U_{MN}} - {U_{NB}})^2}\)

Vậy trong cuộn dây còn có điện trở \(r\)

b) Ta có:

\(\begin{array}{l}U_{MN}^2 = U_r^2 + U_L^2\\ \Rightarrow {U_L} = \sqrt {U_{MN}^2 - U_r^2}  = \sqrt {{{13}^2} - U_r^2} (1)\end{array}\)

\(\begin{array}{l}U_{AB}^2 = {({U_R} + {U_r})^2} + {({U_L} - {U_C})^2}\\ \Leftrightarrow {65^2} = {(13 + {U_r})^2} + {({U_L} - 65)^2}(2)\end{array}\)

Từ (1)(2)\( \Rightarrow {65^2} = {(13 + {U_r})^2} + {(\sqrt {{{13}^2} - U_r^2}  - 65)^2}\)

Giải được \({U_r} = 12V;{U_L} = 5V\)

Hệ số công suất đoạn mạch \(\cos \varphi  = \dfrac{{{U_R} + {U_r}}}{{{U_{AB}}}} = \dfrac{{13 + 12}}{{65}} = \dfrac{5}{{13}}\)