Giải bài 14 trang 96 SGK Toán 10 – Kết nối tri thức
Cho hình vuông ABCD có cạnh bằng a. Gọi M, N tương ứng là trung điểm của các cạnh AB, BC.
Đề bài
Cho hình vuông ABCD có cạnh bằng a. Gọi M, N tương ứng là trung điểm của các cạnh AB, BC.
a) Biểu thị các vecto \(\overrightarrow {DM} ,\overrightarrow {AN} \) theo các vecto \(\overrightarrow {AB} ,\overrightarrow {AD} \)
b) Tính \(\overrightarrow {DM} .\overrightarrow {AN} \) và tìm góc giữa hai đường thẳng DM và AN.
Lời giải chi tiết
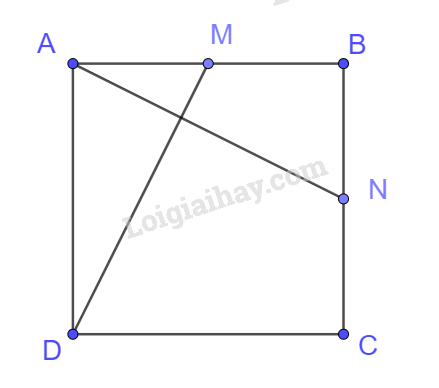
a) Ta có:
\(\overrightarrow {DM} = \overrightarrow {DA} + \overrightarrow {AM} = - \overrightarrow {AD} + \frac{1}{2}\overrightarrow {AB} \) (do M là trung điểm của AB)
\(\overrightarrow {AN} = \overrightarrow {AB} + \overrightarrow {BN} = \overrightarrow {AB} + \frac{1}{2}\overrightarrow {BC} = \overrightarrow {AB} + \frac{1}{2}\overrightarrow {AD} \) (do N là trung điểm của BC)
b)
\(\begin{array}{l}\overrightarrow {DM} .\overrightarrow {AN} = \left( { - \overrightarrow {AD} + \frac{1}{2}\overrightarrow {AB} } \right).\left( {\overrightarrow {AB} + \frac{1}{2}\overrightarrow {AD} } \right)\\ = - \overrightarrow {AD} .\overrightarrow {AB} - \frac{1}{2}{\overrightarrow {AD} ^2} + \frac{1}{2}{\overrightarrow {AB} ^2} + \frac{1}{4}\overrightarrow {AB} .\overrightarrow {AD} \end{array}\)
Mà \(\overrightarrow {AB} .\overrightarrow {AD} = \overrightarrow {AD} .\overrightarrow {AB} = 0\) (do \(AB \bot AD\)), \({\overrightarrow {AB} ^2} = A{B^2} = {a^2};{\overrightarrow {AD} ^2} = A{D^2} = {a^2}\)
\( \Rightarrow \overrightarrow {DM} .\overrightarrow {AN} = - 0 - \frac{1}{2}{a^2} + \frac{1}{2}{a^2} + \frac{1}{4}.0 = 0\)
Vậy \(DM \bot AN\) hay góc giữa hai đường thẳng DM và AN bằng \({90^ \circ }\).
Search google: "từ khóa + timdapan.com" Ví dụ: "Giải bài 14 trang 96 SGK Toán 10 – Kết nối tri thức timdapan.com"







