Bài 139 trang 97 SBT Toán 8 tập 1
Giải bài 139 trang 97 sách bài tập toán 8. Hình thoi ABCD có chu vi bằng 16cm, đường cao AH bằng 2cm. Tính các góc của hình thoi, biết rằng góc A lớn hơn góc B...
Đề bài
Hình thoi \(ABCD\) có chu vi bằng \(16\,cm,\) đường cao \(AH\) bằng \(2\,cm.\) Tính các góc của hình thoi, biết rằng \(\widehat A > \widehat B\)
Phương pháp giải - Xem chi tiết
- Tính độ lớn \(\widehat{HAD}\)
- Tính độ lớn \(\widehat{ADH}\)
- Tính độ lớn các góc còn lại của hình thoi.
Lời giải chi tiết
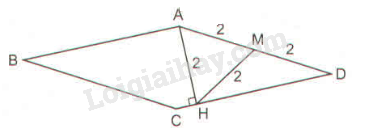
Chu vi hình thoi bằng \(16\, (m)\) nên độ dài một cạnh bằng:
\(16 : 4 = 4 \,(cm)\)
Gọi \(M\) là trung điểm của \(AD.\)
Trong tam giác vuông \(AHD\) ta có \(HM\) là trung tuyến ứng với cạnh huyền
\(HM = AM =\) \(\displaystyle {1 \over 2}\)\(AD=\) \(\displaystyle {1 \over 2}\)\(.4\) \(= 2\, (cm)\)
\(⇒ AH=AM = HM = MD = 2\, cm\)
\(⇒ ∆ AHM\) đều
\( \Rightarrow \widehat {HAM} = {60^0}\) hay \(\widehat {HAD} = {60^0}\)
Trong tam giác vuông \(AHD\) ta có: \(\widehat {HAD} + \widehat D = {90^0}\)
\( \Rightarrow \widehat D = {90^0} - \widehat {HAD}\)\( = {90^0} - {60^0} = {30^0}\)
\( \Rightarrow \widehat B = \widehat D = {30^0}\) (tính chất hình thoi)
Ta có \(AB//CD\) (do ABCD là hình thoi) nên \(\widehat B + \widehat C = {180^0}\) (hai góc trong cùng phía bù nhau)
\( \Rightarrow \widehat C = {180^0} - \widehat B\)\( = {180^0} - {30^0} = {150^0}\)
\(\Rightarrow \widehat A = \widehat C = {150^0}\) (tính chất hình thoi)
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 139 trang 97 SBT Toán 8 tập 1 timdapan.com"







