Bài 138 trang 97 SBT Toán 8 tập 1
Giải bài 138 trang 97 sách bài tập toán 8. Cho hình thoi ABCD, O là giao điểm của hai đường chéo. Gọi E, F, G, H theo thứ tự là chân các đường vuông góc kẻ từ O đến AB, BC, CD, DA...
Đề bài
Cho hình thoi \(ABCD,\, O\) là giao điểm của hai đường chéo. Gọi \(E,\, F,\, G,\, H\) theo thứ tự là chân các đường vuông góc kẻ từ \(O\) đến \(AB,\, BC,\, CD,\, DA.\) Tứ giác \(EFGH\) là hình gì ? Vì sao?
Phương pháp giải - Xem chi tiết
Vận dụng kiến thức : Tứ giác có hai đường chéo bằng nhau và cắt nhau tại trung điểm của mỗi đường là hình chữ nhật.
Lời giải chi tiết
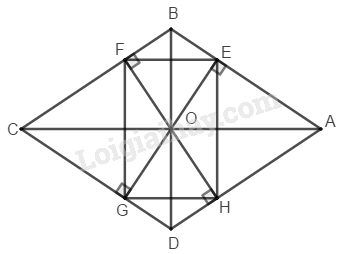
Ta có: \(AB // CD\) (gt)
\(OE ⊥ AB\) (gt)
\(⇒ OE ⊥ CD\)
\(OG ⊥ CD\) (gt)
Suy ra: \(OE\) trùng với \(OG\) nên ba điểm \(O,\, E,\, G\) thẳng hàng.
\(BC // AD\) (gt)
\(OF ⊥ BC\) (gt)
\(⇒ OF ⊥ AD\)
\(OH ⊥ AD\) (gt)
Suy ra: \(OF\) trùng với \(OH\) nên ba điểm \(O,\, H,\, F\) thẳng hàng
Vì \(AC\) và \(BD\) là đường phân giác các góc của hình thoi ABCD, nên ta có:
\(OE = OF\) (tính chất tia phân giác) (1)
\(OE = OH\) (tính chất tia phân giác) (2)
\(OH = OG\) (tính chất tia phân giác) (3)
Từ (1), (2) và (3) suy ra: \(OE = OF = OH = OG\)
Và \(EG=OE+OG=OF+OH=FH\)
Suy ra tứ giác \(EFGH\) có hai đường chéo bằng nhau và cắt nhau tại trung điểm của mỗi đường nên là hình chữ nhật.
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 138 trang 97 SBT Toán 8 tập 1 timdapan.com"







