Bài 1.29 trang 20 SBT hình học 12
Giải bài 1.29 trang 20 sách bài tập hình học 12. Chứng minh rằng mỗi đỉnh của một hình đa diện là đỉnh chung của ít nhất ba cạnh.
Đề bài
Chứng minh rằng mỗi đỉnh của một hình đa diện là đỉnh chung của ít nhất ba cạnh.
Phương pháp giải - Xem chi tiết
Sử dụng định nghĩa hình đa diện:
Hình \(\left( H \right)\) gồm các hữu hạn các đa giác thỏa mãn hai điều kiện:
+ Hai đa giác bất kì hoặc không có điểm chung, hoặc có một đỉnh chung, hoặc có một cạnh chung.
+ Mỗi cạnh của một đa giác là cạnh chung của đúng hai đa giác.
Lời giải chi tiết
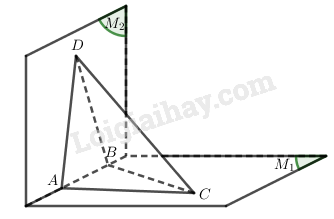
Gọi \({M_1}\) là một mặt của hình đa diện\(\left( H \right)\) chứa ba đỉnh \(A,B,C\).
Khi đó \(AB,BC\) là hai cạnh của \(\left( H \right)\).
Gọi \({M_2}\) là mặt khác với \({M_1}\) và có chung cạnh \(AB\) với \({M_1}\).
Khi đó \({M_2}\) còn có ít nhất một đỉnh \(D\) khác với \(A\) và \(B\).
Nếu \(D \equiv C\) thì \({M_1}\) và \({M_2}\) có hai cạnh chung \(AB\) và \(BC\) (vô lý).
Vậy \(D\) phải khác \(C\). Do đó qua đỉnh \(B\) có ít nhất ba cạnh là \(BA,BC,BD\).
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 1.29 trang 20 SBT hình học 12 timdapan.com"







