Bài 128 trang 96 SBT toán 8 tập 1
Giải bài 128 trang 96 sách bài tập toán 8. Cho điểm A nằm ngoài đường thẳng d. Điểm M di chuyển trên đường thẳng d. Gọi B là điểm đối xứng với A qua M. Điểm B di chuyển trên đường nào ?
Đề bài
Cho điểm \(A\) nằm ngoài đường thẳng \(d.\) Điểm \(M\) di chuyển trên đường thẳng \(d.\) Gọi \(B\) là điểm đối xứng với \(A\) qua \(M.\) Điểm \(B\) di chuyển trên đường nào \(?\)
Phương pháp giải - Xem chi tiết
Ta sử dụng kiến thức:
+) Hai điểm gọi là đối xứng với nhau qua \(O\) nếu \(O\) là trung điểm của đoạn thẳng nối hai điểm đó.
+) Các điểm cách đường thẳng \(b\) một khoảng bằng \(h\) nằm trên hai đường thẳng song song với \(b\) và cách \(b\) một khoảng bằng \(h.\)
Lời giải chi tiết
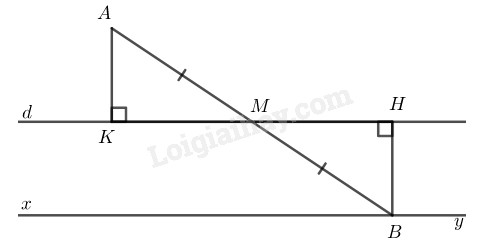
Kẻ \(AK ⊥ d,\) \(BH ⊥ d\)
\(M\) thay đổi trên \(d,\) \(B\) đối xứng với \(A\) qua \(M\) nên \(AM = MB\)
Xét hai tam giác vuông \(AKM\) và \(BHM:\)
\(\widehat {AKM} = \widehat {BHM} = {90^0}\)
\(AM = MB\) (chứng minh trên)
\(\widehat {AMK} = \widehat {BMH}\) (đối đỉnh)
Do đó: \(∆ AKM = ∆ BHM\) (cạnh huyền, góc nhọn) \(⇒ AK = BH\)
Điểm \(A\) cố định, đường thẳng \(d\) cố định nên \(AK\) không thay đổi
\(M\) thay đổi, \(B\) thay đổi cách đường thẳng \(d\) cố định một khoảng bằng \(AK\) không đổi nên \(B\) chuyển động trên đường thẳng \(xy\) song song với \(d\) một khoảng bằng \(AK.\)
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 128 trang 96 SBT toán 8 tập 1 timdapan.com"







