Bài 12 trang 149 Vở bài tập toán 8 tập 1

Đề bài

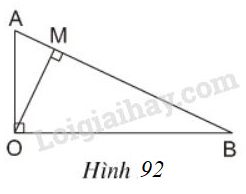
Cho tam giác \(AOB\) vuông tại \(O\) với đường cao \(OM\) (h.\(92\)). Hãy giải thích vì sao ta có đẳng thức:

               \(AB. OM = OA. OB.\)

Lời giải chi tiết

Gọi \(S\) là diện tích tam giác \(AOB\).

Theo công thức tính diện tích tam giác, ta có

\(S = \dfrac{1}{2}AB.OM\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(\,1\,)\)

Theo công thức tính diện tích tam giác vuông, ta có

\(S = \dfrac{1}{2}OA.OB\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(\,2\,)\)

Từ (1) và (2) suy ra \( AB.OM = OA.OB.\)