Bài 1.2 phần bài tập bổ sung trang 156 SBT toán 8 tập 1

LG a

Cho tam giác đều \(ABC.\) Gọi \(M,N,P\) tương ứng là trung điểm của các cạnh \(BC, CA, AB.\) Chứng minh \(MNP\) là tam giác đều.

Phương pháp giải:

Áp dụng tính chất đường trung bình của tam giác

Lời giải chi tiết:

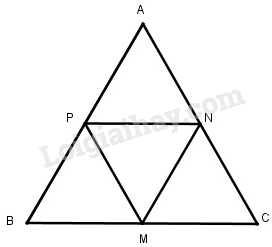
Ta có: \(M\) là trung điểm của \(BC\)

\(N\) là trung điểm của \(AC\)

nên \(MN\) là đường trung bình của \(∆ ABC\)

\(⇒ MN = \dfrac{1}{2} AB\)

Lại có: \(P\) là trung điểm của \(AB\) nên \(MP\) là đường trung bình của \(∆ ABC\)

 \(⇒ MP = \dfrac{1}{2} AC\)

\(NP\) là đường trung bình của \(∆ ABC\)

\(⇒ NP = \dfrac{1}{2} BC\)

Mà \(AB = BC = AC\) (gt) nên \(MN = MP = NP.\) Vậy \(∆ MNP\) đều

LG b

Cho hình vuông \(ABCD.\) Gọi \(M, N, P, Q\) tương ứng là trung điểm của các cạnh \(BC, CD, DA, AB.\) Chứng minh \(MNPQ\) là hình vuông (tứ giác đều)

Phương pháp giải:

Áp dụng tính chất hai tam giác bằng nhau

Lời giải chi tiết:

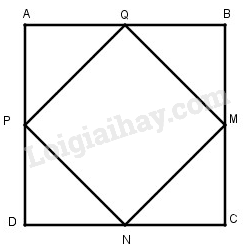
Do ABCD là hình vuông có M, N, P, Q lần lượt là trung điểm của BC, CD, DA, AB nên: \(AQ = QB = BM = MC\)\(= CN = ND = DP = PA\)

Xét \(∆ APQ\) và \(∆ BQM:\)

\(AQ = BQ\) (chứng minh trên)

\(\widehat A = \widehat B = {90^0}\)

\(AP = BM\) (chứng minh trên)

Do đó: \(∆ APQ = ∆ BQM (c.g.c)\) \(⇒ PQ = QM \,(1)\)

Xét \(∆ BQM\) và \(∆ CMN:\)

\(BM = CM\) (chứng minh trên)

\(\widehat B = \widehat C = {90^0}\)

\(BQ = CN \) (chứng minh trên)

Do đó: \(∆ BQM = ∆ CMN (c.g.c)\) \(⇒ QM = MN \,(2)\)

Xét \(∆ CMN\) và \(∆ DNP:\)

\(CN = DN\) (chứng minh trên)

\(\widehat C = \widehat D = {90^0}\)

\(CM = DP\) (chứng minh trên)

Do đó: \(∆ CMN = ∆ DNP (c.g.c)\) \( ⇒ MN = NP \,(3)\)

Từ \((1), (2)\) và \((3)\) suy ra: \(MN = NP = PQ = QM\) nên tứ giác \(MNPQ\) là hình thoi

Vì \(AP = AQ\) nên \(∆ APQ\) vuông cân tại \(A\)

\(BQ = BM\) nên \(∆ BMQ\) vuông cân tại \(B\)

\( \Rightarrow \widehat {AQP} = \widehat {BQM} = {45^0}\)

\(\widehat {AQP} + \widehat {PQM} + \widehat {BQM} = {180^0}\) (kề bù)

\( \Rightarrow \widehat {PQM} = {180^0} - \left( {\widehat {AQP} + \widehat {BQM}} \right)\)

\(= {180^0} - \left( {{{45}^0} + {{45}^0}} \right) = {90^0}\)

Vậy tứ giác \(MNPQ\) là hình vuông.

LG c

Cho ngũ giác đều \(ABCDE. \) Gọi \(M, N, P, Q, R\) tương ứng là trung điểm của các cạnh \(BC, CD, DE, EA, AB.\) Chứng minh \(MNPQR\) là ngũ giác đều.

Phương pháp giải:

Để chứng minh \(MNPQR\) là ngũ giác đều ta cần chứng minh hai điều: hình đó có tất cả các cạnh bằng nhau và có tất cả các góc bằng nhau.

Lời giải chi tiết:

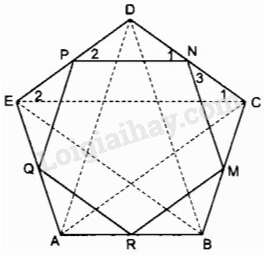
Vì ABCDE là ngũ giác đều nên \(AB=BC=CD\)\(=DE=EA\)

Xét \(∆ ABC\) và \(∆ BCD:\)

\(AB = BC \)(gt)

\(\widehat B = \widehat C\) (gt)

\(BC = CD\) (gt)

Do đó: \(∆ ABC = ∆ BCD (c.g.c)\)

\(⇒ AC = BD\, (1)\)

Xét \(∆ BCD\) và \(∆ CDE:\)

\(BC = CD\) (gt)

\(\widehat C = \widehat D\) (gt)

\(CD = DE\) (gt)

Do đó: \(∆ BCD = ∆ CDE (c.g.c)\) \(⇒ BD = CE \,(2)\)

Xét \(∆ CDE\) và \(∆ DEA:\)

\(CD = DE\) (gt)

\(\widehat D = \widehat E\) (gt)

\(DE = EA\) (gt)

Do đó: \(∆ CDE = ∆ DEA (c.g.c)\) \( ⇒ CE = DA\, (3)\)

Xét \(∆ DEA\) và \(∆ EAB:\)

\(DE = EA\) (gt)

\(\widehat E = \widehat A\) (gt)

\(EA = AB\) (gt)

Do đó: \(∆ DEA = ∆ EAB (c.g.c) \) \(⇒ DA = EB \,(4)\)

Từ \((1), (2), (3), (4)\) suy ra: \(AC = BD = CE = DA = EB\)

Trong \(∆ ABC\) ta có \(RM\) là đường trung bình

\(⇒ RM = \dfrac{1}{2} AC\) (tính chất đường trung bình của tam giác)

Mặt khác, ta có: Trong \(∆ BCD\) ta có \(MN\) là đường trung bình

\(⇒ MN = \dfrac{1}{2} BD\) (tính chất đường trung bình của tam giác)

Trong \(∆ CDE\) ta có \(NP\) là đường trung bình

\(⇒ NP = \dfrac{1}{2} CE\) (tính chất đường trung bình của tam giác)

Trong \(∆ DEA\) ta có \(PQ\) là đường trung bình

\(⇒ PQ = \dfrac{1}{2} DA\) (tính chất đường trung bình của tam giác)

Trong \(∆ EAB\) ta có \(QR\) là đường trung bình

\(⇒ QR = \dfrac{1}{2} EB\) (tính chất đường trung bình của tam giác)

Suy ra: \(MN = NP = PQ = QR = RM\)

Ta có: \(\widehat A = \widehat B = \widehat C = \widehat D = \widehat E\) \( = \dfrac{{(5 - 2){{.180}^0}}}{5}\) \(={108^0}\)

\(∆ DPN\) cân tại \(D\)

\( \Rightarrow \widehat {DPN} = \widehat {DNP}\) \(=\dfrac{{{{108}^0} - \widehat D}}{2}\)  \(=\dfrac{{{{180}^0} - {{108}^{^0}}}}{2}\) \(= {36^0}\)

\(∆ CNM\) cân tại \(C\)

\( \Rightarrow \widehat {CNM} = \widehat {CMN}\) \(=\dfrac{{{{108}^0} - \widehat C}}{2}\) 

\(=\dfrac{{{{180}^0} - {{108}^{^0}}}}{2}\) \(= {36^0}\)

\(\widehat {ADN} + \widehat {PNM} + \widehat {CNM} = {180^0}\)

\( \Rightarrow \widehat {PNM} \\= {180^0} - \left( {\widehat {ADN} + \widehat {CNM}} \right)\)

\(= {180^0} - \left( {{{36}^0} + {{36}^0}} \right) = {108^0}\)

\(∆ BMR\) cân tại \(B\)

\( \Rightarrow \widehat {BMR} = \widehat {BRM} = \dfrac{{{{180}^0} - \widehat B}}{2}\\ = \dfrac{{{{180}^0} - {{108}^0}}}{2} = {36^0}\)

\(\begin{array}{l}\widehat {CNM} + \widehat {NMR} + \widehat {BMR} = {180^0}\\ \Rightarrow \widehat {NMR}\\ = {180^0} - (\widehat {CMN} + \widehat {BMR})\ \\= {180^0} - ({36^0} + {36^0}) = {108^0}\end{array}\)

\(∆ ARQ\) cân tại \(A\)

\(\begin{array}{l}\widehat {{\rm{AR}}Q} = \widehat {AQR} = \dfrac{{{{180}^0} - \widehat A}}{2} \\= \dfrac{{{{180}^0} - {{108}^0}}}{2} = {36^0}\\\widehat {BRM} + \widehat {MRQ} + \widehat {{\rm{AR}}Q} = {180^0}\\ \Rightarrow \widehat {MRQ} = {180^0} - (\widehat {BRM}  + \widehat {{\rm{AR}}Q})\\ = {180^0} - ({36^0} + {36^0}) = {108^0}\end{array}\)

\(∆ QEP\) cân tại \(E\)

\(\begin{array}{l}\widehat {{\rm{EQ}}P} = \widehat {EPQ} = \dfrac{{{{180}^0} - \widehat E}}{2} \\= \dfrac{{{{180}^0} - {{108}^0}}}{2} = {36^0}\\\widehat {AQR} + \widehat {RQB} + \widehat {{\rm{EQ}}P} = {180^0}\\ \Rightarrow \widehat {RQP} = {180^0} - (\widehat {AQR} +  + \widehat {{\rm{EQ}}P})\\ = {180^0} - ({36^0} + {36^0}) = {108^0}\end{array}\)

\(\begin{array}{l}\widehat {EPQ} + \widehat {QPN} + \widehat {DPN} = {180^0}\\ \Rightarrow \widehat {QPN} = {180^0} - (\widehat {EPQ} + \widehat {DPN})\\ = {180^0} - ({36^0} + {36^0}) = {108^0}\end{array}\)

Suy ra : \(\widehat {PNM} = \widehat {NMR} = \widehat {MRQ} \) \( =\widehat {RQP} = \widehat {QPN}\)

Vậy \(MNPQR\) là ngũ giác đều.