Bài 101 trang 92 SBT toán 8 tập 1
Giải bài 101 trang 92 sách bài tập toán 8. Cho góc xOy, điểm A nằm trong góc đó. Vẽ điểm B đối xứng với A qua Ox, vẽ điểm C đối xứng với A qua Oy...
Đề bài
Cho góc \(xOy,\) điểm \(A\) nằm trong góc đó. Vẽ điểm \(B\) đối xứng với \(A\) qua \(Ox,\) vẽ điểm \(C\) đối xứng với \(A\) qua \(Oy.\)
\(a)\) Chứng minh rằng \(OB = OC\)
\(b)\) Tính số đo góc \(xOy\) để \(B\) đối xứng với \(C\) qua \(O.\)
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức:
+) Hai điểm gọi là đối xứng với nhau qua đường thẳng \(d\) nếu \(d\) là đường trung trực của đoạn thẳng nối hai điểm đó.
+) Tính chất đường trung trực: Điểm nằm trên đường trung trực của một đoạn thẳng thì cách đều hai đầu mút của đoạn thẳng đó.
+) Hai điểm gọi là đối xứng với nhau qua \(O\) nếu \(O\) là trung điểm của đoạn thẳng nối hai điểm đó.
+) Trong tam giác cân, đường trung tuyến ứng với cạnh đáy cũng là đường trung trực, đường phân giác.
Lời giải chi tiết
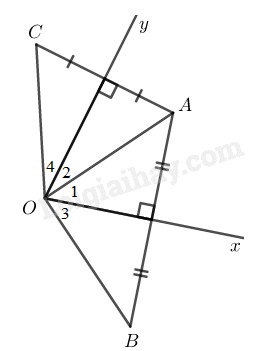
\(a)\) Vì \(B\) đối xứng với \(A\) qua trục \(Ox\) nên \(Ox\) là đường trung trực của đoạn \(AB.\)
\(⇒ OA = OB\) (tính chất đường trung trực) \((1)\)
Vì \(C\) đối xứng với \(A\) qua trục \(Oy\) nên \(Oy\) là đường trung trực của đoạn \(AC.\)
\(⇒ OA = OC\) (tính chất đường trung trực) \((2)\)
Từ \((1)\) và \((2)\) suy ra: \(OB = OC.\)
\(b)\) Ta có: \(OB = OC\) do đó điểm \(B\) đối xứng với điểm \(C\) qua tâm \(O\) cần thêm điều kiện \(B, O, C \) thẳng hàng.
\(∆ OAB\) cân tại \(O\) có \(Ox\) là đường trung trực của \(AB\) nên \(Ox\) cũng là đường phân giác của \(\widehat {AOB} \Rightarrow {\widehat O_1} = {\widehat O_3}\)
\(∆ OAC\) cân tại \(O\) có \(Oy\) là đường trung trực của \(AC\) nên \(Oy\) cũng là đường phân giác của \(\widehat {AOC} \Rightarrow {\widehat O_2} = {\widehat O_4}\)
\(B, O, C\) thẳng hàng \( \Leftrightarrow {\widehat O_1} +{\widehat O_2} + {\widehat O_3} + {\widehat O_4} = {180^0}\)
\(\eqalign{& \Leftrightarrow 2{\widehat O_1} + 2{\widehat O_2} = {180^0} \cr& \Leftrightarrow {\widehat O_1} + {\widehat O_2} = {90^0} \cr& \Leftrightarrow \widehat {xOy} = {90^0} \cr} \)
Vậy \(\widehat {xOy} = {90^0}\) thì \(B\) đối xứng với \(C\) qua tâm \(O.\)
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 101 trang 92 SBT toán 8 tập 1 timdapan.com"







