Đề số 3 - Đề kiểm tra học kì 2 - Toán 7

Đề bài

Câu 1. (3,0 điểm)

Điểm kiểm tra HKI môn toán của học sinh lớp 7 được ghi lại ở bảng sau:

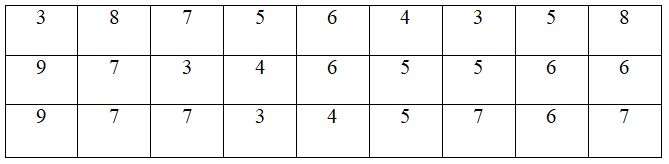
a) Dấu hiệu ở đây là gì? Lớp đó có tất cả bao nhiêu học sinh ?

b) Lập bảng tần số.

c) Tính điểm trung bình môn toán của lớp đó.

Câu 2  (1,0 điểm)

a) Tìm bậc của đơn thức  -2x²y³ 

b) Tìm các đơn thức đồng dạng  trong các đơn thức sau:     

          5xy³; 5x²y³;  -4x³y²; 11 x²y³

Câu 3 (1,5điểm): Cho hai đa thức

P(x) =  4x³ + x²  - x + 5.

Q(x) =  2 x²  + 4x   - 1.

 a) Tính: P(x) + Q(x)

 b) Tính: P(x) -  Q(x)

Câu 4 (1,5 điểm) Cho đa thức A(x)  = x² – 2x .

a) Tính giá trị của  A(x)  tại  x = 2.   

b) Tìm các nghiệm của đa thức A(x).  

Câu 5 (3,0 điểm)

     Cho tam giác ABC cân tại A với đường trung tuyến AH.

a) Chứng minh: \(\Delta AHB = \Delta AHC.\)

b) Chứng minh: \(\widehat {AHB} = \widehat {AHC} = {90^0}.\)

c) Biết AB=AC=13cm, BC = 10 cm, hãy tính độ dài đường trung tuyến AH.

Lời giải chi tiết

Câu 1:

a) Dấu hiệu ở đây là điểm kiểm tra HKI môn toán của học sinh lớp 7. Lớp đó có tất cả 27 học sinh.

b) Bảng tần số:

c) Điểm trung bình môn toán của lớp đó:

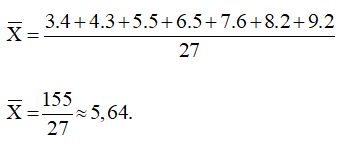
Câu 2:

a) Bậc của đơn thức -2x²y³ là 5.

b) Các đơn thức đồng dạng là 5x²y³ và 11x²y³.

Câu 3:

a) P(x) + Q(x) = 4x³ +3x² + 3x + 4

b) P(x) – Q(x) = 4x³ – x² – 5x + 6

Câu 4:

a) Tại x = 2 ta có:

\(A(2) = {\left( 2 \right)^2} - 2.2 = 0\)

b) \(\begin{array}{l}A(x) = 0\\ \Leftrightarrow {x^2} - 2x = 0\\ \Leftrightarrow x\left( {x - 2} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = 2\end{array} \right.\end{array}\)

Vậy đa thức A(x) có hai nghiệm x = 0 và x = 2

Câu 5: 

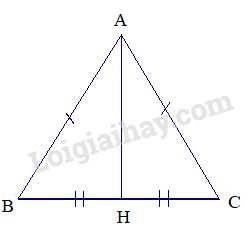
a) Xét \(\Delta AHB\) và \(\Delta AHC\) có:

                         AH  là cạnh chung

                         AB = AC (gt)

                         HB = HC (gt)

\( \Rightarrow \Delta AHB = \Delta AHC\,\,\left( {c.c.c} \right)\)

b) Ta có  \( \Delta AHB = \Delta AHC\,(cmt)\)

Þ \(\widehat {AHB} = \widehat {AHC}\)

Mà:\(\widehat {AHB} + \widehat {AHC} = {180^0}\) (kề bù)

Vậy \(\widehat {AHB} = \widehat {AHC} = \dfrac{{{{180}^0}}}{2} = {90^o}\)

c) Ta có  \(BH = CH = \dfrac{1}{2}.BC = \dfrac{1}{2}.10 = 5\) (cm).

Áp dụng định lí Py-ta-go vào tam giác vuông AHB ta có:

\(\begin{array}{l}A{B^2} = A{H^2} + H{B^2}\\ \Rightarrow A{H^2} = A{B^2} - H{B^2}\\ \Rightarrow A{H^2} = {13^2} - {5^2} = 144\\ \Rightarrow AH = \sqrt {144}  = 12\end{array}\) 

Vậy \(AH=12\) (cm).