Đề kiểm tra 45 phút (1 tiết) - Chương 1 - Đề số 2 - Hình học 10

Đề bài

Câu 1. Cho tam giác ABC. Gọi M, N, P lần lượt là các điểm sao cho \(\overrightarrow {MA}  + \overrightarrow {MB}  = \overrightarrow 0 ,\overrightarrow {NB}  + 2\overrightarrow {NC}  = \overrightarrow 0 ,\)\(\,\overrightarrow {PC}  + 2\overrightarrow {PA}  = \overrightarrow 0 \) .

a.Xác định các điểm M, N, P.

b.Chứng minh rằng với điểm O bất kì ta có \(\overrightarrow {OA}  + \overrightarrow {OB}  + \overrightarrow {OC}  = \overrightarrow {OM}  + \overrightarrow {ON}  + \overrightarrow {OP} \) .

Câu 2. Cho tam giác ABC. Gọi D là điểm trên cạnh BC sao cho \(BD = \dfrac{1}{ 4}BC\) .

Hãy biểu diễn vecto \(\overrightarrow {AD} \) theo hai vecto \(\overrightarrow {AB} ,\overrightarrow {AC} \) .

Câu 3. Cho tam giác ABC vuông tại A có \(AB= 5, AC= 12.\) Tính độ dài của các vecto

a.\(\overrightarrow {AB}  + \overrightarrow {AC} \)

b.\(\overrightarrow {BA}  + \overrightarrow {BC} \) .

Câu 4. Trong mặt phẳng tọa độ Oxy cho ba điểm\(A\left( { - 1' - 2} \right),B\left( {1;2} \right),C\left( {5; - 3} \right)\) .

a.Chứng minh ba điểm A, B, C không thẳng hàng.

b.Tìm tọa độ trọng tâm G của tam giác ABC.

c.Tìm tọa độ điểm D sao cho tam giác ABD nhận C làm trọng tâm.

Lời giải chi tiết

Câu 1.

a.Ta có

\(\eqalign{  & \overrightarrow {MA}  + 2\overrightarrow {MB}  = \overrightarrow 0 \cr& \Leftrightarrow \overrightarrow {MA}  + 2\left( {\overrightarrow {MA}  + \overrightarrow {AB} } \right) = \overrightarrow 0   \cr  & {\rm{                        }} \Leftrightarrow 3\overrightarrow {MA}  + 2\overleftarrow {AB}  = \overrightarrow 0   \cr  & {\rm{                        }} \Leftrightarrow \overrightarrow {AM}  = {2 \over 3}\overrightarrow {AB}  \cr} \) .

Suy ra M là điểm trên cạnh AB sao cho \(AM = {2 \over 3}AB\) .

Tương tự, N là điểm trên cạnh BC sao cho \(BN = {2 \over 3}BC\) , P là điểm trên cạnh CA sao cho \(CP = {2 \over 3}CA\) .

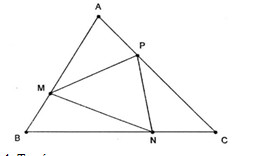
b.Ta có

\(\overrightarrow {OM}  + \overrightarrow {ON}  + \overrightarrow {OP}  \)

\(\;= \overrightarrow {OA}  + \overrightarrow {AM}  + \overrightarrow {OB}  + \overrightarrow {BN}  + \overrightarrow {OC}  + \overrightarrow {CP} \)

\( \;= \overrightarrow {OA}  + \overrightarrow {OB}  + \overrightarrow {OC}  + \dfrac{2 }{3}\overrightarrow {AB}  + \dfrac{2}{3}\overrightarrow {BC}  + {2 \over 3}\overrightarrow {CA} \)

\(\eqalign{  &  = \overrightarrow {OA}  + \overrightarrow {OB}  + \overrightarrow {OC}  + {2 \over 3}\left( {\overrightarrow {AB}  + \overrightarrow {BC}  + \overrightarrow {CA} } \right)  \cr  &  = \overrightarrow {OA}  + \overrightarrow {OB}  + \overrightarrow {OC}  \cr} \)

Câu 2.

Ta có: \(\eqalign{  & \overrightarrow {BD}  = {1 \over 4}\overrightarrow {BC}\cr&  \Leftrightarrow \overrightarrow {AD}  - \overrightarrow {AB}  = {1 \over 4}\left( {\overrightarrow {AC}  - \overrightarrow {AB} } \right)  \cr  & {\rm{                  }} \Leftrightarrow \overrightarrow {AD}  = {3 \over 4}\overrightarrow {AB}  + {1 \over 4}\overrightarrow {AC}  \cr} \)

Câu 3.

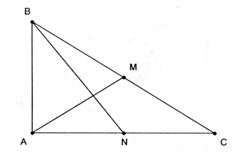
Gọi M là trung điểm BC, N là trung điểm AC.

Ta có

\(\eqalign{  & \left| {\overrightarrow {AB}  + \overrightarrow {AC} } \right| = \left| {2\overrightarrow {AM} } \right| = 2AM = BC  \cr  & {\rm{                }} = \sqrt {A{B^2} + A{C^2}}  = \sqrt {25 + 144}  = 13 \cr} \) .

\(\left| {\overrightarrow {BA}  + \overrightarrow {BC} } \right| = \left| {2\overrightarrow {BN} } \right| = 2BN \)\(\,= \sqrt {A{B^2} + A{N^2}}  = \sqrt {25 + 36}  = \sqrt {61} \) .

Câu 4 

a.Ta có \(\overrightarrow {AB}  = \left( {2,4} \right),\overrightarrow {AC}  = \left( {6; - 1} \right)\) . Suy ra \(\overrightarrow {AB} ,\overrightarrow {AC} \) không cùng phương.

Vậy A, B, C không thẳng hàng.

b. Ta có \(\left\{ \matrix{  {x_G} = \dfrac{{{x_A} + {x_B} + {x_C}}}{3} = \dfrac{5}{3} \hfill \cr {y_G} = \dfrac{{{y_A} + {y_B} + {y_C}}}{3} =  - 1 \hfill \cr}  \right.\)

Vậy \(G = \left( \dfrac{5}{3}; - 1 \right)\) .

c. Ta có \(\left\{ \matrix{ {x_C} = \dfrac{{{x_A} + {x_B} + {x_D}}}{3} \hfill \cr  {y_C} = \dfrac{{{y_A} + {y_B} + {y_D}}}{3}\hfill \cr}  \right. \)

\(\Rightarrow \left\{ \matrix{  {x_D} = 3{x_C} - {x_A} - {x_B} = 15 \hfill \cr  {y_D} = 3{y_C} - {y_A} - {y_B} =  - 9 \hfill \cr}  \right.\)

Vậy \(D = \left( {15; - 9} \right)\) .