Đề kiểm tra 45 phút (1 tiết) - Chương 1 - Đề số 1 - Hình học 10

Đề bài

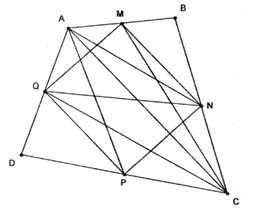
Câu 1. Cho tứ giác lồi ABCD. Gọi M, N, P, Qlần lượt là trung điểm AB, BC, CD, DA. Chứng minh rằng

a.Chứng minh rằng \(\overrightarrow {MP}  = \dfrac{1 }{ 2}\left( {\overrightarrow {AD}  + \overrightarrow {BC} } \right)\) .

b.Hai tam giác ANP và CMQ có cùng trọng tâm.

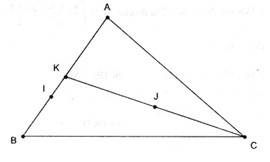
Câu 2. Cho tam giác ABC. Xác định các điểm I, J sao cho

\(\overrightarrow {IA}  + 2\overrightarrow {IB}  = \overrightarrow 0 ,\)\(\,\overrightarrow {JA}  + \overrightarrow {JB}  + 2\overrightarrow {JC}  = \overrightarrow 0 \) .

Câu 3. Cho hai điểm cố định A, B. Tìm tập hợp các điểm M sao cho

\(\left| {\overrightarrow {MA}  + \overrightarrow {MB} } \right| = \left| {\overrightarrow {MA}  - \overrightarrow {MB} } \right|\) .

Câu 4. Trong mặt phẳng tọa độ Oxy cho ba điểm \(A(1;2), B(-3;-2), C(5;-1).\)

A.Chứng minh A, B, C là ba đỉnh của một tam giác.

b.Tìm tọa độ của véc tơ trung tuyến \(\overrightarrow {AM} \) của tam giác ABC.

c.Tìm tọa độ điểm D sao cho ABCD là hình bình hành.

Lời giải chi tiết

Câu 1.

 

a. \(\dfrac{1 }{2}\left( {\overrightarrow {AD}  + \overrightarrow {BC} } \right) \)

\(= \dfrac{1 }{ 2}\left( {\overrightarrow {AM}  + \overrightarrow {MP}  + \overrightarrow {PD}  + \overrightarrow {BM}  + \overrightarrow {MP}  + \overrightarrow {PC} } \right)\)

\( = \dfrac{1 }{ 2}\left( {2\overrightarrow {MP}  + \overrightarrow {AM}  + \overrightarrow {BM}  + \overrightarrow {PC}  + \overrightarrow {PD} } \right)\)

\(= \overrightarrow {MP} \)

b. Theo tính chất đường trung bình \(\overrightarrow {MN}  = \dfrac{1}{ 2}\overrightarrow {AC} ,\overrightarrow {PQ}  = \dfrac{1 }{2}\overrightarrow {AC} \) .

Gọi G là trọng tâm tam giác ANP. Ta có \(\overrightarrow {GA}  + \overrightarrow {GN}  + \overrightarrow {GP}  = \overrightarrow 0 \) .

Suy ra:

\(\overrightarrow {GC}  + \overrightarrow {GM}  + \overrightarrow {GQ}  \)

\(= \overrightarrow {GA}  + \overrightarrow {AC}  + \overrightarrow {GN}  + \overrightarrow {MN}  + \overrightarrow {GP}  + \overrightarrow {PQ} \)

\( = \overrightarrow {GA}  + \overrightarrow {GN}  + \overrightarrow {GP}  + \overrightarrow {AC}  - \dfrac{1 }{ 2}\overrightarrow {AC}  - \dfrac{1 }{ 2}\overrightarrow {AC}  = \overrightarrow 0 \)

Vậy G là trọng tâm tam giác CNQ.

Câu 2.

Ta có:

\(\eqalign{  & \overrightarrow {IA}  + 2\overrightarrow {IB}  = \overrightarrow 0 \cr& \Leftrightarrow \overrightarrow {IA}  + 2\left( {\overrightarrow {IA}  + \overrightarrow {AB} } \right) = \overrightarrow 0   \cr  & {\rm{                   }} \Leftrightarrow 3\overrightarrow {IA}  + 2\overrightarrow {AB}  \Leftrightarrow \overrightarrow {AI}  = {2 \over 3}\overrightarrow {AB}  \cr} \) .

Suy ra I là điểm trên cạnh AB sao cho \(AI = \dfrac{2 }{ 3}AB\).

Gọi K là trung điểm AB. Ta có

\(\overrightarrow {JA}  + \overrightarrow {JB}  + 2\overrightarrow {JC}  = \overrightarrow 0\)

\(  \Leftrightarrow 2\overrightarrow {JK}  + 2\overrightarrow {JC}  = \overrightarrow 0 \)

\(\Leftrightarrow \overrightarrow {JK}  + \overrightarrow {JC}  = \overrightarrow 0 \)

Suy ra J là trung điểm KC.

 

Câu 3.

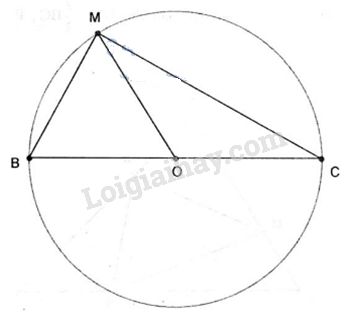
Gọi O là trung điểm AB.

Ta có: \(\left| {\overrightarrow {MA}  + \overrightarrow {MB} } \right| = \left| {\overrightarrow {MA}  - \overrightarrow {MB} } \right| \)

\(\Leftrightarrow \left| {2\overrightarrow {MO} } \right| = \left| {\overrightarrow {BA} } \right|\)

\(\Leftrightarrow MO = \dfrac{1 }{ 2}AB\) .

M cách O cố định một đoạn không đổi bằng \(\dfrac{1 }{ 2}AB\) nên tập hợp các điểm M là đường trong tâm O bán kính \(\dfrac{1 }{2}AB\) hay có đường kính là AB.

Câu 4.

a.Ta có \(\overrightarrow {AB}  = \left( { - 4; - 4} \right),\overrightarrow {AC}  = \left( {4; - 3} \right)\) .

Mà \(\dfrac{{ - 4}}{{ - 4}} \ne \dfrac{{ - 4}}{{ - 3}}\) . Suy ra \(\overrightarrow {AB} ,\overrightarrow {AC} \) không cùng phương.

Vậy A, B, C không thẳng hàng hay A, B, C là ba đỉnh của một tam giác.

b.Gọi M là trung điểm BC. Tọa độ của M là \(\left( {\dfrac{{{x_B} + {x_c}}}{2};\dfrac{{{y_B} + {y_C}}}{2}} \right) = \left( {1; - \dfrac{3}{2}} \right).\)

Suy ra \(\overrightarrow {AM}  = \left( {0; - {7 \over 2}} \right)\) .

c. ABCD là hình bình hành khi và chỉ khi \(\overrightarrow {DC}  = \overrightarrow {AB} \) .

Mà \(\overrightarrow {DC}  = \left( {5 - {x_D}; - 1 - {y_D}} \right),\)\(\,\overrightarrow {AB}  = \left( { - 4, - 4} \right)\) .

Do đó \(\left\{ \matrix{  5 - {x_D} =  - 4 \hfill \cr   - 1 - {y_D} =  - 4 \hfill \cr}  \right. \Leftrightarrow \left\{ \matrix{  {x_D} = 9 \hfill \cr  {y_D} = 3 \hfill \cr}  \right.\) .

 Vậy \(D = \left( {9;3} \right)\) .