Đề kiểm tra 15 phút - Đề số 19 - Bài 2,3,4,5 - Chương 2 - Hình học 7

Đề bài

Cho tam giác ABC, D là trung điểm của AB. Đường thẳng qua D và song song với BC cắt AC ở E. Đường thẳng qua E và song song với AB cắt BC ở F. Chứng minh rằng:

a) \(AD = EF \)

b) \(\Delta ADE = \Delta EFC.\)

Lời giải chi tiết

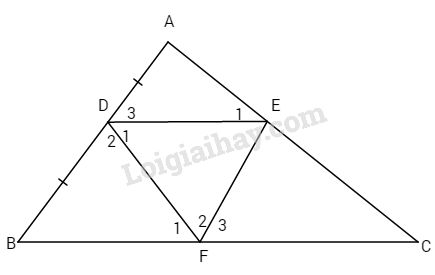
a) Ta có DE // BC (giả thiết) \( \Rightarrow \widehat {{D_1}} = \widehat {{F_1}}\)  (1) (cặp góc so le trong)

Tương tự EF // AD \( \Rightarrow \widehat {{D_2}} = \widehat {{F_2}}\)  (2)

Xét \(\Delta BDF \) và \( \Delta EFD\) có: DF là cạnh chung và (1), (2)

\(\Rightarrow \Delta BDF = \Delta EFD\) (g.c.g)

\( \Rightarrow BD = EF\) (cạnh tương ứng)  (3)

Lại có D là trung điểm của AB (giả thiết)

\( \Rightarrow AD = BD\)

Từ (3), (4) \( \Rightarrow AD = EF\)

b) DE // BC \( \Rightarrow \widehat {{E_1}} = \widehat C\)(cặp góc đồng vị). Tương tự \( \Rightarrow \widehat {{D_3}} = \widehat B.\)

Do đó \(\widehat {{D_3}} = \widehat {{F_3}}.\)

Mặt khác \(\Delta BDF = \Delta EFD\) (chứng minh trên)

\( \Rightarrow BF = DE,\) mà \(BF = CF\) (giả thiết)

\( \Rightarrow DE = CF\)

Do đó \(\Delta ADE = \Delta EFC\) (g.c.g).