Đề kiểm tra 15 phút - Đề số 5 - Bài 5 - Chương 2 - Hình học 9
Giải Đề kiểm tra 15 phút - Đề số 5 - Bài 5 - Chương 2 - Hình học 9
Đề bài
Cho tam giác ABC, các đường cao AD, BE và CF. Gọi H là trực tâm của tam giác.
a. Chứng minh bốn điểm A, E, H, F cùng nằm trên một đường tròn xác định tâm I
b. Gọi O là trung điểm của BC. Chứng minh OE là tiếp tuyến của đường tròn (I).
Lời giải chi tiết
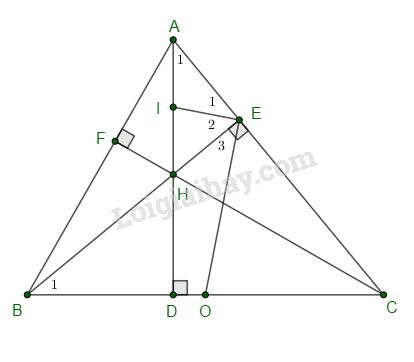
a. Ta có: \(\widehat {AFH} = \widehat {AEH} = 90^\circ \) (gt)
⇒ E, F nằm trên đường tròn đường kính AH có tâm I là trung điểm đoạn AH.
b. ∆BEC vuông tại E có O là trung điểm của BC (gt)
\( \Rightarrow OE = OB = {{BC} \over 2}\) nên \({\widehat E_3} = {\widehat B_1};{\widehat B_1} = {\widehat A_1}\) (cùng phụ với góc C)
∆AIE cân \( \Rightarrow {\widehat A_1} = {\widehat E_1}.\) Do đó \({\widehat E_3} = {\widehat E_1},\) mà \({\widehat E_1} + {\widehat E_2} = 90^\circ \) (gt)
\( \Rightarrow {\widehat E_3} + {\widehat E_2} = 90^\circ \) hay OE là tiếp tuyến của (I)
Search google: "từ khóa + timdapan.com" Ví dụ: "Đề kiểm tra 15 phút - Đề số 5 - Bài 5 - Chương 2 - Hình học 9 timdapan.com"







