Đề kiểm tra 15 phút - Đề số 1 - Bài 9 - Chương 3 – Hình học 7

Đề bài

Cho tam giác ABC (AB = AC), hai đường cao BE và CF cắt nhau tại H (E thuộc AC và F thuộc AB). Tia AH cắt BC ở I. Chứng minh:

a) I là trung điểm của BC.

b) \(\Delta IEF\) cân.

Lời giải chi tiết

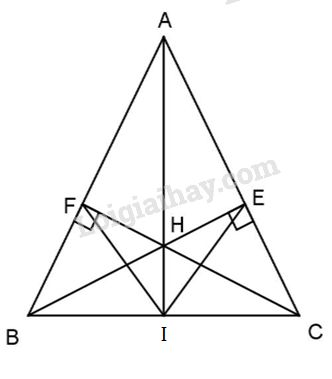
a) Hai đường cao BE và CF cắt nhau tại H nên H là trực tâm của \(\Delta ABC\). Do đó AH là đường cao thứ ba, AH cắt BC ở I nên \(AI \bot BC.\)

\(\Delta ABC\) cân tại A (gt) đường cao AI đồng thời là đường trung tuyến , hay I là trung điểm của BC.

b) Hai tam giác vuông BFC và CEB có trung cạnh huyền BC nên hai trung tuyến: \(FI = EI\) hay \(\Delta IEF\) cân.