Đề kiểm tra 15 phút - Đề số 1 - Bài 11 - Chương 1 - Hình học 8

Đề bài

Cho tứ giác ABCD có AD = BC. Gọi I, J lần lượt là trung điểm của các cạnh AB và CD; K, H theo thứ tự là trung điểm của hai đường chéo AC và BD. Chứng minh rằng: \(IJ \bot HK.\)

Lời giải chi tiết

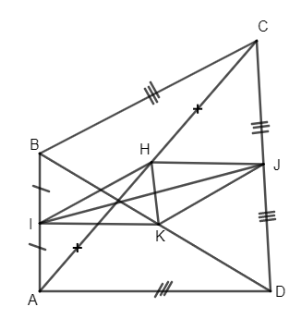
Ta có I, H là trung điểm của AB và AC nên IH là đường trung bình của  \(\Delta ABC \Rightarrow IH = \dfrac{1 }{ 2}BC\)  (1)

Lại có JK là đường trung bình của \(\Delta BCD\) nên \(JK = \dfrac{1}{ 2}BC\)  (2)

Từ (1) và (2) \( \Rightarrow IH = JK = \dfrac{1}{ 2}BC\)

Chưng minh tương tự ta có: \(JH = IK = \dfrac{1}{ 2}AD\) mà AD = BC (gt)

\( \Rightarrow IH = HJ = JK = KI.\)

Do đó IHJK là hình thoi (bốn cạnh bằng nhau) \( \Rightarrow IJ \bot HK.\)