Đề số 6 - Đề kiểm tra học kì 2 - Vật lí 11

Đề bài

Câu 1 (3 điểm).

Hai dòng điện có cường độ \({I_1}\, = \,12\,A;\,{I_2}\, = \,18A\) chạy trong hai dây dẫn thẳng dài vô hạn, song song, cách nhau a = 5 cm trong chân không, ngược chiều nhau.

a) Xác định cảm ứng từ tại điểm M cách I₁ một khoảng 3cm, cách I₂ một khoảng 2cm.

b) Tìm quỹ tích các điểm tại đó cảm ứng từ bằng 0.

c) Tại điểm M ở câu (a) đặt một dòng điện I₃ = 5A song song với hai dòng điện trên, cùng chiều I₁. Tính lực từ tác dụng lên 1m chiều dài của dòng điện I₃.

Câu 2 (3 điểm).

Một êlectron (điện tích q = -1,6.10^-19 C; khối lượng m = 9,1.10^-31 kg) chuyển động với vận tốc v₀ = 36 km/s đi vào trong một từ trường đều có \(\overrightarrow B \) vuông góc với \(\overrightarrow {{v_0}} .\)

a) Tính lực Lo-ren-xơ tác dụng lên êlectron biết B = 2,5 T.

b) Cho biết dạng quỹ đạo của êlectron. Tính bán kính quỹ đạo và chu kì quay của êlectron.

Câu 3 (4 điểm).

Một ống dây dài 30cm, đường kính 2cm, có 1500 vòng dây.

a) Tính độ tự cảm của ống dây.

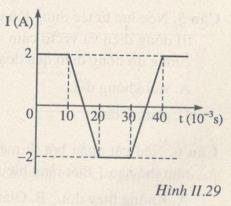
b) Cường độ dòng điện trong ống dây đó biến thiên đều theo thời gian theo đồ thị hình II.29. Vẽ đồ thị suất điện động tự cảm xuất hiện trong ống dây phụ thuộc thời gian.

c) Tính độ biến thiên năng lượng từ trường trong ống dây trong 0,04s đầu.

 

Lời giải chi tiết

Câu 1:

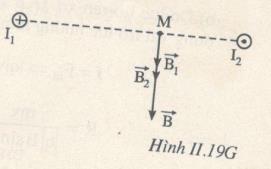
a) Tại M có \({\overrightarrow B _1},\,{\overrightarrow B _2}\) do I₁, I₂ gây ra, có chiều xác định bằng quy tắc nắm tay phải và biểu diễn trên hình II.19G.

\(\begin{array}{l}{\overrightarrow B _M} = {\overrightarrow B _1} + {\overrightarrow B _2}\\ + \,{B_1} = {2.10^{ - 7}}.\dfrac{{{I_1}}}{{{r_1}}} = {2.10^{ - 7}}.\dfrac{{12}}{{0,03}} = {8.10^{ - 5}}T.\\ + \,{B_2} = {2.10^{ - 7}}.\dfrac{{{I_2}}}{{{r_2}}} = {2.10^{ - 7}}.\dfrac{{18}}{{0,02}} = {18.10^{ - 5}}T.\end{array}\)

Nhận thấy \({\overrightarrow B _1},{\overrightarrow B _2}\) cùng phương cùng chiều nên \({\overrightarrow B _M}\) cùng phương, cùng chiều \({\overrightarrow B _1}\) và \({B_M} = {B_1} + {B_2} = {26.10^{ - 5}}T.\)

 

b) Gọi N là điểm mà tại đó \({\overrightarrow B _N} = \overrightarrow 0  \Rightarrow {\overrightarrow B _N} = {\overrightarrow B _1} + {\overrightarrow B _2} = \overrightarrow 0 \)

\( \Rightarrow \,{\overrightarrow B _1},\,{\overrightarrow B _2}\) cùng phương, ngược chiều, cùng độ lớn.

+ \({\overrightarrow B _1},{\overrightarrow B _2}\) cùng phương, ngược chiều => N phải ở ngoài khoảng I₁I₂.

+ B₁ = B­₂

\(\begin{array}{l} \Rightarrow \,{2.10^{ - 7}}.\dfrac{{{I_1}}}{{{r_1}}} = {2.10^{ - 7}}.\dfrac{{{I_2}}}{{{r_2}}}\\ \Rightarrow {r_2} = \dfrac{{{I_2}}}{{{I_1}}}{r_1} = 1,5{r_1}\end{array}\)

 

=> N ở ngoài khoảng I₁I₂ và bên trái I₁.

Mặt khác \({r_1} + 5 = 1,5{r_1}\, \Rightarrow \,{r_1} = 10\,cm.\)

Vậy quỹ tích các điểm tại đó cảm ứng từ bằng 0 là đường thẳng song song, đồng phẳng với hai dòng điện, ngoài khoảng hai dòng điện và cách I₁ 10 cm.

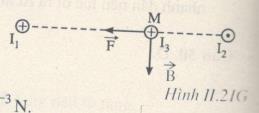
c) Áp dụng quy tắc ban tay trái xác định phương, chiều của lực từ tác dụng lên I₃ đặt tại M biểu diễn như hình II.21G.

B_M = 26.10^-5 T.

Ta có \(F = {B_M}{I_3}{l_3}\sin \alpha  = {26.10^{ - 5}}.5.1.1 = 1,{3.10^{ - 3}}\,N.\)

 

Câu 2:

a) \({v_0} = 36\,km/s = {36.10^3}\,m/s.\)

\(f = \left| q \right|vB\sin \alpha  = 1,{6.10^{ - 19}}{.36.10^3}.2,5.1\)\(\, = 1,{44.10^{ - 14}}\,N.\)

b) Do lực Lo-ren-xơ \(\overrightarrow f  \bot \overrightarrow v \) nên điện tích chuyển động tròn đều, lực Lo-ren-xơ đóng vai trò lực hướng tâm.

\(\begin{array}{l}f = {F_{ht}}\,\\ \Rightarrow \,\left| q \right|vB\sin \alpha  = \dfrac{{m{v^2}}}{R}\, \\ \Rightarrow \,\left| q \right|B\sin \alpha  = \dfrac{{mv}}{R}\\ \Rightarrow R = \dfrac{{mv}}{{\left| q \right|B\sin \alpha }} \\\;\;\;\;\;\;\;\;= \dfrac{{9,{{1.10}^{ - 31}}{{.36.10}^3}}}{{1,{{6.10}^{ - 19}}.2,5.1}} \\\;\;\;\;\;\;\;\;\;= 8,{19.10^{ - 9}}\,m.\end{array}\)

Chu kì quay: \(T\, = \,\dfrac{{2\pi R}}{v} = \dfrac{{2\pi .8,{{19.10}^{ - 9}}}}{{{{36.10}^3}}} = 1,{43.10^{ - 12}}\)

Câu 3:

\(\begin{array}{l}a)\,L\, = \,4\pi {.10^{ - 7}}.\dfrac{{{N^2}S}}{l}\\ \Rightarrow L\, = \,4\pi {.10^{ - 7}}.\dfrac{{{{1500}^2}.\pi .0,{{01}^2}}}{{0,3}} = 2,{96.10^{ - 3}}\,H.\end{array}\)

 

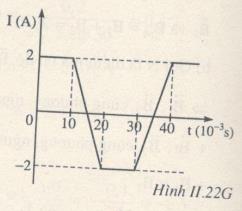
b) + Từ 0 đến 10.10^-3s: I = 2A

\( \Rightarrow \Delta I = 0\, \Rightarrow \,{e_{tc}} =  - L\dfrac{{\Delta I}}{{\Delta t}} = 0\)

+ Từ 10.10^-3s đến 20.10^-3s:

I giảm từ 2A đến -2A.

\(\begin{array}{l} \Rightarrow {e_{tc}} =  - L\dfrac{{\Delta I}}{{\Delta t}} =  - 2,{96.10^{ - 3}}.\dfrac{{ - 2 - 2}}{{0,01}}\\ = 1,184\,V.\end{array}\)

+ Từ 20.10^-3s đến 30.10^-3s \( \Rightarrow I\, = \, - 2A\)

\( \Rightarrow \Delta I = 0 \Rightarrow {e_{tc}} =  - L\dfrac{{\Delta I}}{{\Delta t}} = 0\)

+ Từ 30.10^-3s đến 40.10^-3s:

I tăng từ -2A đến 2A.

\( \Rightarrow {e_{tc}} =  - L\dfrac{{\Delta I}}{{\Delta t}} \)\(\,=  - 2,{96.10^{ - 3}}.\dfrac{{2 - ( - 2)}}{{0,01}} =  - 1,184\,V.\)

Đồ thị e_tc theo thời gian biểu diễn như hình vẽ.

 

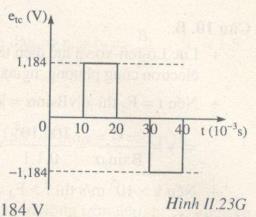
c) t = 0 => I = 2A

Năng lượng từ trường trong ống dây:

\({{\rm{W}}_1} = \dfrac{1}{2}L{I^2} = \dfrac{1}{2}.2,{96.10^{ - 3}}{.2^2} = 5,{92.10^{ - 3}}\,J;\)

\(\,t = \,0,04s;\,I\, = 2A\, \Rightarrow {{\rm{W}}_2} = {{\rm{W}}_1}\)

=> Độ biến thiên năng lượng từ trường \(\Delta \,{\rm{W}}\, = \,0.\)