Câu 83 trang 130 Sách bài tập Hình học 11 Nâng cao

Đề bài

Cho hình lập phương ABCD.A’B’C’D’ cạnh a. Gọi I là điểm thuộc AB; đặt \(AI = x\left( {0 < x < a} \right)\).

a) Khi góc giữa hai đường thẳng AC’ và DI bằng 60°, hãy xác định vj trí của điểm I.

b) Tính theo a và x diện tích thiết diện của hình lập phương khi cắt bởi mặt phẳng (B’DI). Tìm x để diện tích ấy là nhỏ nhấ.

c) Tính khoảng cách từ đến mặt phẳng (B’DI) theo a và x.

Lời giải chi tiết

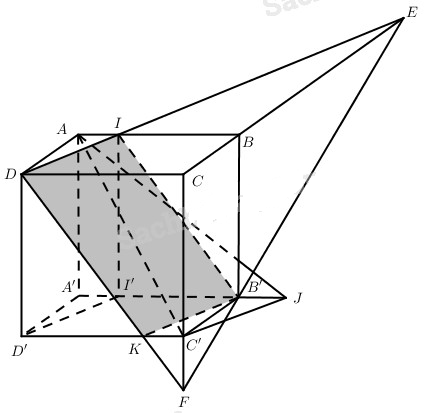
a) Cách 1.

Đặt α là góc giữa DI và AC’ thì

\(\eqalign{  & \cos \alpha  = {{\left| {\overrightarrow {DI} .\overrightarrow {AC'} } \right|} \over {\left| {\overrightarrow {DI} } \right|.\left| {\overrightarrow {AC'} } \right|}}  \cr  &  = {{\left( {\overrightarrow {DA}  + \overrightarrow {AI} } \right)\left( {\overrightarrow {AD}  + \overrightarrow {AB}  + \overrightarrow {AA'} } \right)} \over {\left| {\overrightarrow {DI} } \right|.\left| {\overrightarrow {AC'} } \right|}}  \cr  &  = {{\left| { - {a^2} + xa} \right|} \over {\sqrt {{a^2} + {x^2}.a\sqrt 3 } }} = {{\left| { - a + x} \right|} \over {\sqrt 3 .\sqrt {{a^2} + {x^2}} }} \cr} \)

Khi ấy \(\alpha  = {60^0}\) khi và chỉ khi

\(\eqalign{  & {{\left| { - a + x} \right|} \over {\sqrt 3 .\sqrt {{a^2} + {x^2}} }} = {1 \over 2}  \cr  &  \Leftrightarrow {x^2} - 8ax + {a^2} = 0  \cr  &  \Leftrightarrow x = a\left( {4 - \sqrt {15} } \right)\,\,\,\left( {vì\,\,0 < x < a} \right) \cr} \)

Hệ thức trên xác định vị trí điểm I.

Cách 2.

Kẻ \(II'//AA'\left( {I' \in A'B'} \right),C'J//D'I'\) (I’ thuộc đường thẳng A’B’) thì \(\widehat {AC'J}\) hoặc \({180^0} - \widehat {AC'J}\) là góc giữa hai đường thẳng AC’ và DI với B’J = x.

Do giả thiết góc giữa hai đường thẳng AC’ và DI bằng 60° nên \(\widehat {AC'J} = {60^0}\) hoặc 120°.

Ta có :

\(\eqalign{  & A{J^2} = AA{'^2} + A'{J^2} = {a^2} + {\left( {a + x} \right)^2}  \cr  & AC{'^2} = 3{a^2},C'{J^2} = {a^2} + {x^2} \cr} \)

- Trường hơp \(\widehat {AC'J} = {60^0}\), ta có

\(A{J^2} = AC{'^2} + C'{J^2} - 2AC'.C'J.{1 \over 2}\)

hay

\(\eqalign{& {a^2} + {\left( {a + x} \right)^2} \cr & = 3{a^2} + {a^2} + {x^2} - 2a\sqrt 3 .\sqrt {{a^2} + {x^2}.{1 \over 2}} \cr & \Leftrightarrow {x^2} - 8ax + {a^2} = 0 \cr & \Rightarrow x = \left( {4 - \sqrt {15} } \right)a\,\,\left( {vì\,0 < x < a} \right) \cr}\)

Trường hợp \(\widehat {AC'J} = {120^0}\), ta có

\(\eqalign{& {a^2} + {\left( {a + x} \right)^2} \cr & = 3{{\rm{a}}^2} + {a^2} + {x^2} + 2{\rm{a}}\sqrt 3 .\sqrt {{a^2} + {x^2}} .{1 \over 2} \cr & \Leftrightarrow 2ax = 2{a^2} + a\sqrt 3 .\sqrt {{a^2} + {x^2}} \cr & \Leftrightarrow 2\left( {x - a} \right) = \sqrt 3 .\sqrt {{a^2} + {x^2}} \cr} \)

Điều này không xảy ra vì 0 < x < a.

Vậy khi \(x = \left( {4 - \sqrt {15} } \right)a\) thì góc giữa DI và AC’ bằng 60°.

b) Gọi

\(\eqalign{  & E = DI \cap CB  \cr  & F = B'E \cap CC'  \cr  & K = DF \cap D'C' \cr} \)

thì thiết diện của hình lập phương khi cắt bởi mp(B’DI) là tứ giác DIB’K.

Dễ thấy đó là hình bình hành

\({S_{DIB'K}} = 2{{\rm{S}}_{B'I{\rm{D}}}}\)

\(= 2.{1 \over 2}\sqrt {{{\overrightarrow {IB'} }^2}.{{\overrightarrow {I{\rm{D}}} }^2} - {{\left( {\overrightarrow {IB'} .\overrightarrow {I{\rm{D}}} } \right)}^2}} \)

Mặt khác \({\overrightarrow {I{\rm{D}}} ^2}.{\overrightarrow {IB'} ^2} = \left( {{a^2} + {x^2}} \right)\left[ {{a^2} + {{\left( {a - x} \right)}^2}} \right]\)

và \(\eqalign{  & {\left( {\overrightarrow {I{\rm{D}}} .\overrightarrow {IB'} } \right)^2} = {\left[ {\left( {\overrightarrow {IA}  + \overrightarrow {A{\rm{D}}} } \right)\left( {\overrightarrow {IB}  + \overrightarrow {BB'} } \right)} \right]^2}  \cr  &  = {\left( {\overrightarrow {IA} .\overrightarrow {IB} } \right)^2} = {\left[ { - x{{\left( {a - x} \right)}^2}} \right]^2} = {x^2}{\left( {a - x} \right)^2} \cr} \)

Từ đó

\(\eqalign{  & {S_{DIB'K}} = \sqrt {{a^4} + {a^2}{x^2} + {a^2}{{\left( {a - x} \right)}^2}}   \cr  &  = a\sqrt {{a^2} + {x^2} + {{\left( {a - x} \right)}^2}}  \cr} \)

Dễ thấy \({S_{DIB'K}}\) đạt giá trị nhỏ nhất khi \(x = {a \over 2}\) .

c) Gọi khoảng cách từ C đến mp(B’ID), do tứ diện CDEF có CD, CE , CF đôi một vuông góc nên

\({1 \over {{h^2}}} = {1 \over {C{{\rm{D}}^2}}} + {1 \over {C{E^2}}} + {1 \over {C{F^2}}}\).

Mặt khác do AD // BE nên \({a \over {BE}} = {x \over {a - x}}\).

từ đó \(BE = {{a\left( {a - x} \right)} \over x}\)

và \(CE = a + {{a\left( {a - x} \right)} \over x} = {{{a^2}} \over x}\).

Tương tự như trên, ta có \(C'F = {{ax} \over {a - x}}\) từ đó

\(CF = a + {{ax} \over {a - x}} = {{{a^2}} \over {a - x}}\).

Như vậy \({1 \over {{h^2}}} = {1 \over {{a^2}}} + {{{x^2}} \over {{a^4}}} + {{{{\left( {a - x} \right)}^2}} \over {{a^4}}}\)

do vậy \(h = {{{a^2}} \over {\sqrt {{a^2} + {x^2} + {{\left( {a - x} \right)}^2}} }}\)