Câu 72 trang 128 Sách bài tập Hình học 11 Nâng cao
Giải bài tập Câu 72 trang 128 Sách bài tập Hình học 11 Nâng cao
Đề bài
Cho hình lăng trụ tam giác ABC.A’B’C’. Lấy các điểm \({A_1},{B_1},{C_1}\) lần lượt thuộc các cạnh bên AA’, BB’, CC’ sao cho \({{A{A_1}} \over {AA'}} = {{B'{B_1}} \over {BB'}} = {{C'{C_1}} \over {CC'}} = {3 \over 4}\). Trên các đoạn thẳng CA1 và A’B1 lần lượt lấy các điểm I, J sao cho IJ // B’C1. Tính tỉ số \({{IJ} \over {B'{C_1}}}\) .
Lời giải chi tiết
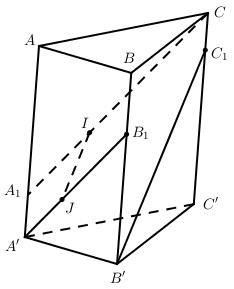
Đặt \(\overrightarrow {AA'} = \overrightarrow a ,\overrightarrow {AB} = \overrightarrow b ,\overrightarrow {AC} = \overrightarrow c \). Theo giả thiết ta có:
\(\overrightarrow {A{A_1}} = {3 \over 4}\overrightarrow a ,\overrightarrow {B'{B_1}} = - {3 \over 4}\overrightarrow a ,\overrightarrow {C'{C_1}} = - {3 \over 4}\overrightarrow a .\)
Ta có:
\(\eqalign{ & \overrightarrow {C{A_1}} = \overrightarrow {CA} + \overrightarrow {A{A_1}} \cr & = {3 \over 4}\overrightarrow a - \overrightarrow c ; \cr & \overrightarrow {A'{B_1}} = \overrightarrow {A'B'} + \overrightarrow {B'{B_1}} \cr & = - {3 \over 4}\overrightarrow a + \overrightarrow b ; \cr & \overrightarrow {B'{C_1}} = \overrightarrow {B'A'} + \overrightarrow {A'C'} + \overrightarrow {C'{C_1}} \cr & = - {3 \over 4}\overrightarrow a - \overrightarrow b + \overrightarrow c \cr} \)
Vì I thuộc CA1 nên \(\overrightarrow {CI} = t\overrightarrow {C{A_1}} = {3 \over 4}t\overrightarrow a - t\overrightarrow c .\)
Do J thuộc A’B1 nên \(\overrightarrow {A'J} = m\overrightarrow {A'{B_1}} = - {3 \over 4}m\overrightarrow a + m\overrightarrow b \) .
Mặt khác
\(\eqalign{ & \overrightarrow {IJ} = \overrightarrow {IC} + \overrightarrow {CA'} + \overrightarrow {A'J} \cr & = - {3 \over 4}t\overrightarrow a + t\overrightarrow c + \overrightarrow a - \overrightarrow c - {3 \over 4}m\overrightarrow a + m\overrightarrow b \cr & = \left( {1 - {3 \over 4}t - {3 \over 4}m} \right)\overrightarrow a + m\overrightarrow b + \left( {t - 1} \right)\overrightarrow c \cr} \)
Ta có:
\(\eqalign{ & IJ//B'{C_1} \Leftrightarrow \overrightarrow {IJ} = k\overrightarrow {B'{C_1}} \cr & \Leftrightarrow \left\{ \matrix{ 1 - {3 \over 4}t - {3 \over 4}m = - {3 \over 4}k \hfill \cr m = - k \hfill \cr t - 1 = k \hfill \cr} \right. \cr} \)
Suy ra
\(\eqalign{ & 1 - {3 \over 4}\left( {k + 1} \right) + {3 \over 4}k = - {3 \over 4}k \cr & \Leftrightarrow {1 \over 4} + {3 \over 4}k = 0 \Leftrightarrow k = - {1 \over 3} \cr & \Rightarrow t = {2 \over 3},m = {1 \over 3}. \cr} \)
Vậy điểm I thuộc A1C được xác định bởi \(\overrightarrow {CI} = {2 \over 3}\overrightarrow {C{A_1}} \) và J thuộc A’B1 được xác định \(\overrightarrow {A'J} = {1 \over 3}\overrightarrow {A'{B_1}} \).
Khi đó, ta có \({{IJ} \over {B'{C_1}}} = {1 \over 3}.\)
Search google: "từ khóa + timdapan.com" Ví dụ: "Câu 72 trang 128 Sách bài tập Hình học 11 Nâng cao timdapan.com"