Câu 65 trang 62 - 63 Sách Bài tập Hình học 11 Nâng cao

Đề bài

Cho hình hộp ABCD.A₁B₁C₁D₁.

a) Hãy xác định đường thẳng \(\Delta \) cắt cả hai đường thẳng AC₁ và BA₁ đồng thời song song với B₁D₁.

b) Gọi I, J lần lượt là giao điểm của  với AC₁ và BA₁. Tính tỉ số \({{AI} \over {A{C_1}}}\).

Lời giải chi tiết

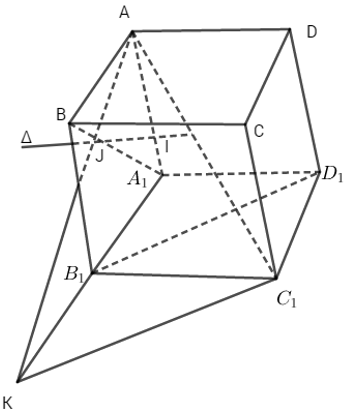
a) Giả sử đã xác định được đường thẳng \(\Delta \) cắt AC₁ và BA₁ lần lượt tại I và J.

Xét phép chiếu song song lên mp(ABB₁A₁) theo phương chiếu D₁B₁. Khi đó, hình chiếu của ba điểm thẳng hàng A, I, C₁ lần lượt là ba điểm thẳng hàng A, J, K. Mặt khác J thuộc BA₁, nên J chính là giao điểm của AK và BA₁.

Từ đó, ta có cách dựng đường thẳng \(\Delta \) theo các bước sau đây:

- Dựng điểm K là hình chiếu của C₁ (theo phương chiếu D₁B₁).

- Lấy giao điểm J của AK và BA₁.

- Qua J dựng đường thẳng \(\Delta \) // C₁K ( đã có C₁K // B₁D₁) ta được đường thẳng \(\Delta \) cần tìm.

b) Dễ thấy \({A_1}{B_1} = {B_1}K \Rightarrow {A_1}K = 2AB\) (do A₁B₁ = AB).

Vì AB // A₁K \( \Rightarrow {{{\rm{AJ}}} \over {JK}} = {{AB} \over {{A_1}K}} = {1 \over 2}\).

Mặt khác IJ // C₁K \( \Rightarrow {{AI} \over {I{C_1}}} = {{{\rm{AJ}}} \over {JK}} = {1 \over 2} \Rightarrow {{AI} \over {A{C_1}}} = {1 \over 3}\).