Câu 65 trang 127 Sách bài tập Hình học 11 Nâng cao

Đề bài

a) Hai mặt phẳng ABC và ABD của hình tứ diện ABCD là những tam giác có diện tích bằng nhau. Chứng minh rằng đường vuông góc chung của AB và CD đi qua trung điểm của CD.

b) Bốn mặt của hình tứ diện ABCD có diện tích bằng nhau. Chứng minh rằng các cặp đối diện của tứ diện bằng nhau, nghĩa là BC = AD, AC = BD, AB = CD.

Lời giải chi tiết

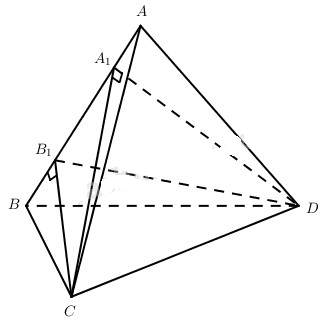
a) 

Vì \({S_{CAB}} = {S_{DAB}}\) nên \(C{B_1} = D{A_1}\) (CB₁, DA₁ tương ứng là đường cao của các tam giác CAB và DAB). Từ đó \(C{A_1} = D{B_1}\).

Nếu A₁ \( \ne \) B₁

Xét tứ diện A₁B₁CD có \({A_1}C = {B_1}D,C{B_1} = D{A_1}\) nên đường vuông góc chung của A₁B­₁, CD là đường thẳng nối trung điểm của A₁B₁ và CD, hay đường vuông góc chung của AB và CD đi qua trung điểm của CD.

Nếu A₁ ≡ B₁ thì kết quả là hiển nhiên.

Cách 2.

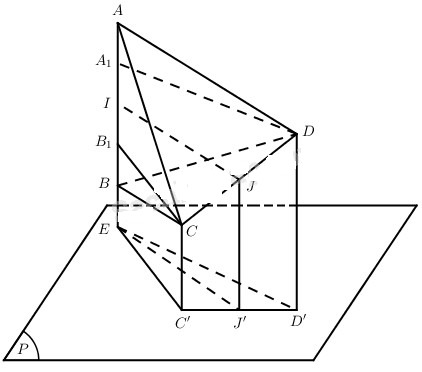
Kẻ các đường cao CB₁, DA₁ tương ứng của tam giác CAB và DAB. Xét mp(P) vuông góc với AB. Gọi IJ là đường vuông góc với AB. Gọi IJ là đường vuông góc chung của AB và CD thì IJ // (P), CB₁ // (P) và DA₁ // (P).

Chiếu tứ diện đã cho lên (P) thì các điểm A, B, A₁, B₁, I cùng có hình chiếu là E. Các điểm C, J, D lần lượt có hình chiếu là C’, J’, D’. Dễ thấy J’ thuộc  \(C'D',EC' = C{B_1},E{\rm{D}}' = {A_1}D\) từ đó EC’ = ED’.

Mặt khác do \(IJ \bot AB\) và \(IJ \bot CD\) nên suy ra \(EJ' \bot C'D'\).

Như vậy C’ED’ là tam giác cân tại E và nhận EJ’ là đường cao, từ đó J’C’ = J’D’.

Do  vậy JC = JC, tức là đường vuông góc chung của AB, CD đi qua trung điểm của CD.

b) Vì bốn mặt của tứ diện ABCD có diện tích bằng nhau nên \({S_{CAB}} = {S_{DAB}}\) và \({S_{BC{\rm{D}}}} = {S_{AC{\rm{D}}}}\). Do đó theo câu a) thì đường vuông góc chung của AB và CD là đường thẳng IJ, trong đó I và J lần lượt là trung điểm của AB và CD. Khi đó AC = BD, BC = AD.

Tương tự như trên ta có AC = BD và AB = CD. Vậy ABCD là tứ diện có các cặp cạnh đối diện bằng nhau, tức là AB = CD, AC = BD, AD = BC.