Câu 57 trang 125 Sách bài tập Hình học 11 Nâng cao

Đề bài

Cho hình chóp S.ABC có đáy là tam giác vuông ở C, cạnh SA vuông góc với mặt phẳng đáy, \(AC = a,BC = b,SA = h\). Gọi M và N lần lượt là trung điểm của các cạnh AC và SB.

a) Tính độ dài MN.

b) Tìm hệ thức liên hệ giữa a, b, h để MN là đường vuông góc chung của AC và SB.

Lời giải chi tiết

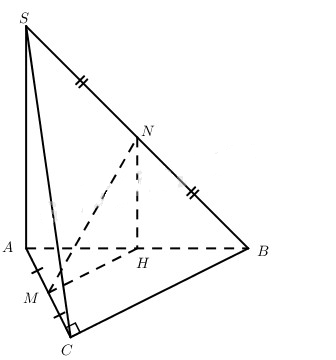
a) Gọi H là trung điểm của AB thì NH // SA.

Do \(SA \bot \left( {ABC} \right)\) nên \(NH \bot \left( {ABC} \right)\), từ đó \(\widehat {NHM} = {90^0}\). Vậy

\(\eqalign{  & M{N^2} = N{H^2} + H{M^2}  \cr  &  = {{S{A^2}} \over 4} + {{B{C^2}} \over 4} = {1 \over 4}\left( {{h^2} + {b^2}} \right)  \cr  &  \Rightarrow MN = {1 \over 2}\sqrt {{h^2} + {b^2}}  \cr} \)

b) h = b