Câu 64 trang 126 Sách bài tập Hình học 11 Nâng cao
Giải bài tập Câu 64 trang 126 Sách bài tập Hình học 11 Nâng cao
Đề bài
Trong mặt phẳng (P) cho đường tròn (C) đường kính AB = 2R; C là điểm bất kì thuộc đường tròn (C không trùng với A, B). S là điểm trong không gian sao cho SA vuông góc với (P) và SA = h (h cho trước và h < 2R). Gọi I và J lần lượt là trung điểm của AC và SB. Hãy xác định vị trí điểm C trên đường tròn để IJ là đường vuông góc chung của AC và SB. Khi đó, tính khoảng cách từ điểm A đến mp(SBC).
Lời giải chi tiết
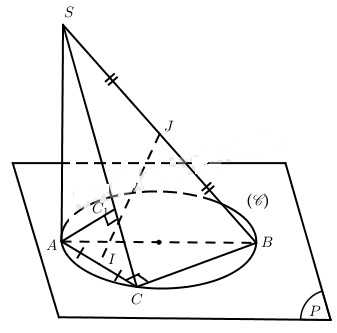
Cách 1:
Dễ thấy ACB là tam giác vuông tại C mà \(SA \bot \left( {ABC} \right)\) nên \(\widehat {SCB} = {90^0}\). Tam giác SAB vuông tại A, tam giác SCB vuông tại C mà J là trung điểm của SB, từ đó AJ = CJ. Mặt khác IA = IC. Vậy \(IJ \bot AC\). Từ đó, IJ là đường vuông góc chung của AC và SB khi và chỉ khi IS = IB. Xét các tam giác vuông SAI và BCI ta thấy IS = IB khi và chỉ khi SA = BC.
Vậy điểm C thuộc đường tròn đã cho sao cho BC = h thì IJ là đường vuông góc chung của AC và SB. Chú ý rằng có hai điểm C như vậy.
Cách 2:
Xét tứ diện SABC với I, J là trung điểm của AC, SB ta có IJ là đường vuông góc chung của AC và SB khi và chỉ khi SA = CB và SC = AB.
Xét các tam giác vuông SAC và ACB ta có các đẳng thức trên xảy ra khi và chỉ khi SA = BC.
Dễ thấy \(d\left( {A;mp\left( {SCB} \right)} \right) = A{C_1}\), trong đó AC1 là đường cao của tam giác vuông SAC.
Ta có \(A{C_1} = {{SA.AC} \over {SC}}\)
mà \(AC = \sqrt {4{{\rm{R}}^2} - {h^2}} ,SC = 2{\rm{R}}\)
Từ đó, ta có \(A{C_1} = {{h\sqrt {4{{\rm{R}}^2} - {h^2}} } \over {2{\rm{R}}}}\)
Search google: "từ khóa + timdapan.com" Ví dụ: "Câu 64 trang 126 Sách bài tập Hình học 11 Nâng cao timdapan.com"







