Bài 57 trang 14 SBT Hình Học 11 Nâng cao

Đề bài

Cho hai đường tròn (O) và (O^’) cắt nhau tại A và B. Một đường thẳng thay đổi đi qua A cắt (O) ở A và M, cắt (O^’) tại A và M^’. Gọi P và P^’ lần lượt là trung điểm của AM và AM^’.

a) Tìm quỹ tích trung điểm I của đoạn thẳng PP^’.

b) Tìm quỹ tích trung điểm J của đoạn thẳng MM^’.

Lời giải chi tiết

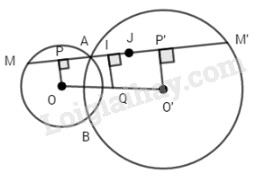
a) Gọi Q là trung điểm của OO^’ thì QI\( \bot \)IA. Suy ra quỹ tích I là đường tròn đường kính AQ.

b) Vì J là trung điểm MM^’ nên

\(\overrightarrow {AJ}  = {1 \over 2}\left( {\overrightarrow {AM}  + \overrightarrow {AM'} } \right)\)

\( = \overrightarrow {AP}  + \overrightarrow {AP'}  = 2\overrightarrow {AI} \)

Vậy phép vị tự tâm A tỉ số 2 biến điểm I thành điểm J. Do đó, quỹ tích J là ảnh của đường tròn đường kính AQ qua phép vị tự đó.